§ 1.5. Суперпозиція логічних функцій
Логічні функції АБО-НЕ, заборона а, заборона b, нерівнозначність, І-НІ, рівнозначність є несамостійними і можуть бути виражені через операції інверсії, кон’юнкції, диз’юнкції. Таким чином, і будь-яку функцію можна представити через операції інверсії, кон’юнкції, диз’юнкції. За законом де Моргана, кон’юнкція може бути виражена через диз’юнкцію і навпаки, тобто будь-яка логічна функція може бути виражена за допомогою двох логічних функцій: І-НЕ, АБО-НЕ.
Повна система – це система логічних функцій, за допомогою яких може бути виражена будь-яка логічна функція у вигляді суперпозицій функції цієї системи.
Максимальна система – повний набір всіх елементарних логічних функцій.
Для логічних схем І, АБО, НЕ існують типові технічні схеми, які реалізують їх на дискретних напівпровідникових елементах. Для побудови сучасних ЕОМ звичайно застосовуються системи інтегральних елементів, у котрих з ціллю більшої уніфікації у якості базової логічної схеми використовується одна із схем І-НЕ, АБО-НЕ, І-АБО-НЕ.
Мінімальна повна система – це система, видалення з якої хоча б однієї функції перетворює її в неповну.
Можна виділити 4 мінімальні повні системи:
І, НЕ;
АБО, НЕ;
І-НЕ;
АБО-НЕ.
Приклад.
Задана функція Х. Реалізувати Х у базисах І, НЕ; АБО, НЕ; І-НЕ; АБО-НЕ.
.
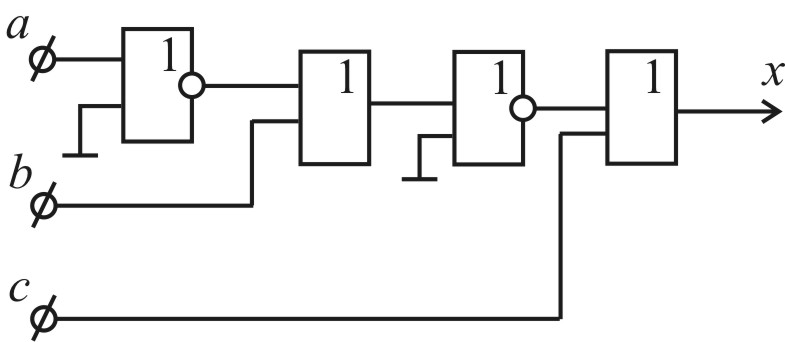
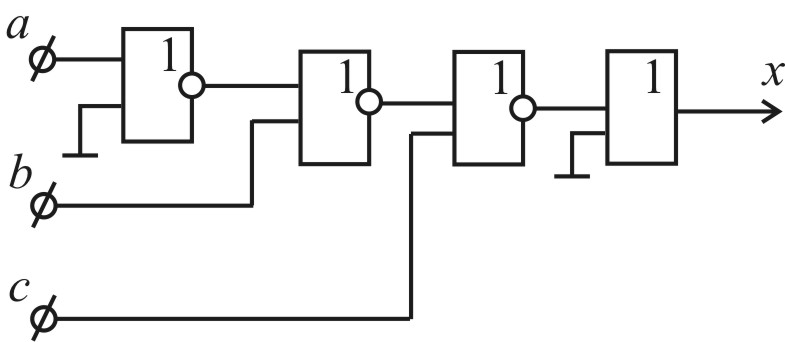
1) у базисі І-НЕ:
|
2) у базисі АБО, НЕ:
|
.
.
3) у базисі І, НЕ:
|
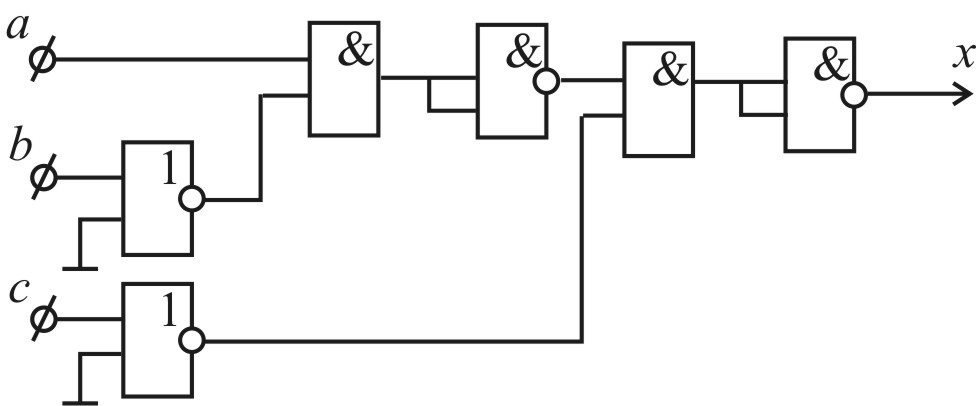
4) у базисі АБО-НЕ:
|
5) у змішаному базисі:
|
|
.
§ 1.6. Нормальні і досконалі нормальні форми логічних функцій
Будь-яка логічна функція може бути представлена у вигляді диз’юнктивної нормальної форми (ДНФ – диз’юнкція елементарних кон’юнкцій) та кон’юнктивної нормальної форми (КНФ – кон’юнкція елементарних диз’юнкцій).
Елементарними кон’юнкціями називаються кон’юнкції будь-якого числа різних змінних, узятих з інверсіями або без них.
Аналогічно елементарними диз’юнкціями називаються диз’юнкції будь-якого числа змінних, узятих з інверсіями або без них.
Для усякої логічної функції можуть існувати декілька рівносильних ДНФ і КНФ.
Інверсія будь-якої логічної функції, записаної у вигляді Дні КНФ, може бути представлена, навпаки, у вигляді КНФ або ДНФ шляхом заміни операцій множення на складання та складання на множення.
-
елементарні диз’юнкції;
-
елементарні кон’юнкції.
ДНФ:
;
КНФ:
.
Існує вид ДНФ та КНФ, у якому логічна функція може бути записана єдиним чином. Це досконала нормальна форма.
Досконалою диз’юнктивною нормальною формою (ДДНФ) э диз’юнкція елементарних кон’юнкцій, які містять всі змінні з інверсіями або без них.
Досконалою кон’юнктивною нормально формою (ДКНФ) є кон’юнкція елементарних диз’юнкцій, які містять всі змінні з інверсіями або без них.
ДДНФ записується по одиницям за допомогою таблиць істинності:
a |
b |
c |
x |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
.
ДКНФ записується по нулям. До тієї ж таблиці:
.
КНФ ті ДНФ можна привести до ДДНФ та ДКНФ.
Приклад.
Приведемо
ДНФ
до ДДНФ за допомогою закону доповнення:
.
Знайдені набори 111, 110, 101 відповідають десятинним числам 7, 6 та 2.
.
Приведемо
КНФ
до ДКНФ:
Знайдені набори 000, 001, 100 відповідають десятинним числам 0,1 і 5.
Властивості досконалих нормальних форм:
Якщо логічна функція при даному наборі змінних приймає нульове значення, то при цьому ж наборі жодна елементарна кон’юнкція її ДДНФ не приймає єдиного значення.
Якщо логічна функція при даному наборі змінних приймає одиничне значення, то при цьому ж наборі тільки одна елементарна кон’юнкція її ДДНФ приймає значення одиниці.
Якщо логічна функція при даному наборі змінних приймає нульове значення, то тільки одна елементарна диз’юнкція її ДКНФ приймає нульове значення при даному наборі.
Якщо логічна функція приймає одиничне значення, то жодна з елементарних диз’юнкцій її ДКНФ не приймає нульового значення при даному наборі.