
- •Вопросы для подготовки к экзамену по теории вероятностей и математической статистике
- •Факториал числа
- •Формулировка комбинаторных правил суммы и произведения. Четыре комбинаторных схемы выбора. Формулы для числа размещений и сочетаний в разных схемах выбора. Число перестановок.
- •Правило произведения
- •Перестановки
- •Размещения
- •Сочетания
- •3.Классическое, геометрическое и статистическое определения вероятности. Вывод свойств вероятности из определений. Ограниченность классических определений вероятности.
- •2) Устойчивость относительных частот появления а в различных сериях достаточно
- •4. Вероятностное пространство (ω, s, р). Аксиомы теории вероятностей и следствия из них. Описание конечного вероятностного пространства в аксиоматике Колмогорова.
- •Вероятностные пространства (в расширенном смысле и бесконечные)
- •5.Условная вероятность. Определение зависимых и независимых событий. Попарная незевисимость событий и независимость в совокупности.
- •Независимость событий
- •Независимость событий в совокупности
- •6.Теорема о вероятности суммы событий. Формула полной вероятности. Вероятность гипотез: постановка задачи. Формулы Байеса для вероятностей гипотез.
- •Формула Байеса (теорема гипотез).
- •7. Определение случайной величины. Закон распределения вероятностей случайной величины. Способы задания дискретной случайной величины. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •Дискретные случайные величины
- •8. Функция распределения случайной величины, ее свойства и график. Функция распределения.
- •9.Непрерывные случайные величины. Способы задания непрерывной случайной величины. Плотность вероятности и ее основные свойства.
- •10.Числовые характеристики дискретных и непрерывных случайных величин. Математическое ожидание случайной величины и его свойства. Дисперсия случайной величины и её свойства.
- •1. Параметры уравнения регрессии.
4. Вероятностное пространство (ω, s, р). Аксиомы теории вероятностей и следствия из них. Описание конечного вероятностного пространства в аксиоматике Колмогорова.
Вероятностное пространство —
это тройка
![]() ,
где:
,
где:
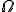 —
это множество объектов
—
это множество объектов
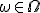 ,
называемых элементарными исходами
эксперимента. На это множество
не накладывается никаких условий, оно
может быть совершенно произвольным.
При задании вероятностной модели для
конкретного случайного эксперимента
множество
необходимо
определять таким образом, чтобы в любой
реализации опыта происходил один и
только один элементарный исход.
Элементарный исход содержит в себе всю
возможную информацию о результате
случайного опыта. С формальной
математической точки зрения «произвести
случайный опыт» означает в точности
указать один элементарный исход
,
называемых элементарными исходами
эксперимента. На это множество
не накладывается никаких условий, оно
может быть совершенно произвольным.
При задании вероятностной модели для
конкретного случайного эксперимента
множество
необходимо
определять таким образом, чтобы в любой
реализации опыта происходил один и
только один элементарный исход.
Элементарный исход содержит в себе всю
возможную информацию о результате
случайного опыта. С формальной
математической точки зрения «произвести
случайный опыт» означает в точности
указать один элементарный исход
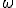 ,
который произошел в данной реализации
опыта.
,
который произошел в данной реализации
опыта.
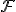 —
это некоторая зафиксированная система
подмножеств
—
это некоторая зафиксированная система
подмножеств
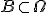 ,
которые будут называться (случайными)
событиями. Если элементарный
исход, произошедший в результате
реализации случайного опыта, входит в
событие
,
которые будут называться (случайными)
событиями. Если элементарный
исход, произошедший в результате
реализации случайного опыта, входит в
событие
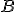 ,
то говорят, что в данной реализации
событие
произошло,
иначе говорят, что событие не произошло.
Совокупность событий
должна
быть сигма-алгеброй, то есть удовлетворять
следующим свойствам:
,
то говорят, что в данной реализации
событие
произошло,
иначе говорят, что событие не произошло.
Совокупность событий
должна
быть сигма-алгеброй, то есть удовлетворять
следующим свойствам:
Пустое множество
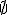 должно
быть событием, то есть принадлежать
.
Это событие, которое существует в любом
вероятностном пространстве, называется
невозможным, поскольку оно никогда
не происходит.
должно
быть событием, то есть принадлежать
.
Это событие, которое существует в любом
вероятностном пространстве, называется
невозможным, поскольку оно никогда
не происходит.
Все множество также должно быть событием:
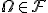 .
Это событие называется достоверным,
так как происходит при любой реализации
случайного опыта.
.
Это событие называется достоверным,
так как происходит при любой реализации
случайного опыта.
Совокупность событий должна образовывать алгебру, то есть быть замкнутой относительно основных теоретико-множественных операций, выполняемых над конечным числом событий. Если
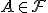 и
и
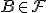 ,
тогда должно быть
,
тогда должно быть
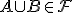 ,
,
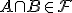 ,
,
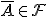 .
Операции над событиями имеют очевидный
содержательный смысл.
.
Операции над событиями имеют очевидный
содержательный смысл.
В дополнение к указанным свойствам, система должна быть замкнута относительно операций над событиями, выполняемых в счетном числе (свойство сигма-алгебры). Если
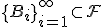 ,
тогда должно быть
,
тогда должно быть
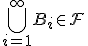 и
и
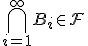 .
.
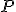 —
это числовая функция, которая определена
на
и
ставит в соответствие каждому событию
число
—
это числовая функция, которая определена
на
и
ставит в соответствие каждому событию
число
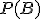 ,
которое называется вероятностью
события
.
Эта функция должна быть конечной
сигма-аддитивной мерой, равной 1 на всем
пространстве, то есть обладать свойствами:
,
которое называется вероятностью
события
.
Эта функция должна быть конечной
сигма-аддитивной мерой, равной 1 на всем
пространстве, то есть обладать свойствами:
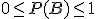 для
любого
для
любого
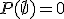 ,
,
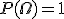
Если и — события, причем
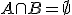 ,
тогда
,
тогда
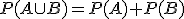 (свойство
аддитивности).
(свойство
аддитивности).
Если , причем Если
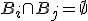 для
любых Если
для
любых Если
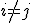 ,
тогда должно быть
,
тогда должно быть
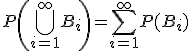 (свойство
сигма-аддитивности).
(свойство
сигма-аддитивности).
Заметим, что последнее свойство сигма-аддитивности меры эквивалентно (при условии выполнения всех прочих свойств, в том числе конечной аддитивности) любому из следующих свойств непрерывности меры:
Если
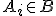 и
и
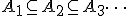 ,
тогда
,
тогда
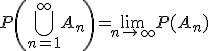 .
.
Если и
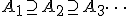 ,
тогда
,
тогда
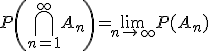 .
.
Если , и
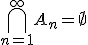 ,
тогда
,
тогда
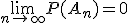 .
.
Пусть
![]() —
множество элементов
—
множество элементов
![]() ,
которые называются элементарными
событиями, а
,
которые называются элементарными
событиями, а
![]() —
множество подмножеств
,
называемых случайными событиями (или
просто — событиями), а
—
пространством элементарных событий.
—
множество подмножеств
,
называемых случайными событиями (или
просто — событиями), а
—
пространством элементарных событий.
Аксиома I (алгебра событий). является алгеброй событий.
Аксиома II (существование вероятности событий). Каждому событию x из поставлено в соответствие неотрицательное действительное число
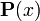 ,
которое называется вероятностью события
x.
,
которое называется вероятностью события
x.Аксиома III (нормировка вероятности).
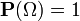 .
.Аксиома IV (аддитивность вероятности). Если события x и y не пересекаются, то
![]() .
.
Совокупность объектов
![]() ,
удовлетворяющая аксиомам I—IV,
называется вероятностным
пространством (у Колмогорова:
поле вероятностей).
,
удовлетворяющая аксиомам I—IV,
называется вероятностным
пространством (у Колмогорова:
поле вероятностей).
Система аксиом I—IV непротиворечива.
Это показывает следующий пример:
состоит
из единственного элемента
,
—
из
и
множества невозможных событий (пустого
множества)
![]() ,
при этом положено
,
при этом положено
![]() .
Однако эта система аксиом не является
полной: в разных вопросах теории
вероятностей рассматриваются различные
вероятностные пространства.
.
Однако эта система аксиом не является
полной: в разных вопросах теории
вероятностей рассматриваются различные
вероятностные пространства.
