Сочетания

Сочетания без повторений — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.

 

формула для нахождения количества сочетаний без  повторений:

 

Сочетания с повторениями — комбинаторные соединения из n элементов по m, составленные из этих элементов без учета порядка с возможностью многократного повторения предметов.

 

формула для нахождения количества сочетаний с  повторениями:

2.Испытания и события. Виды и типы событий. Пространство элементарных событий. Определения суммы, произведения и разности событий, противоположного события. Изображение событий на диаграммах Эйлера-Венна.

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

О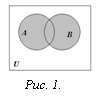 пределение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

 

О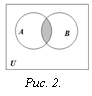 пределение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

 

О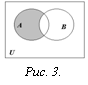 пределение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

 

О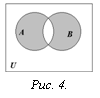 пределение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

Определение 2.1. Противоположными событиями называют два несовместных события,

образующих полную группу. Если одно из них назвать А, то второе принято обозначать

А .

Замечание. Таким образом, А заключается в том, что событие А не произошло.

Теорема 2.2. Сумма вероятностей противоположных событий равна 1:

р(А) + р( А ) = 1.

3.Классическое, геометрическое и статистическое определения вероятности. Вывод свойств вероятности из определений. Ограниченность классических определений вероятности.

Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их

число равно п ( число возможных исходов), а при т из них происходит некоторое событие

А (число благоприятных исходов).

Определение 1.8. Вероятностью события А называется отношение числа исходов опыта,

благоприятных этому событию, к числу возможных исходов:

п

р(А) т - - классическое определение вероятности.

Свойства вероятности.

Из определения 1.8 вытекают следующие свойства вероятности:

Свойство 1. Вероятность достоверного события равна единице.

Доказательство. Так как достоверное событие всегда происходит в результате опыта, то

все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно,

Р(А) = 1.

Свойство 2. Вероятность невозможного события равна нулю.

Доказательство. Для невозможного события ни один исход опыта не является благопри-

ятным, поэтому т = 0 и р(А) = 0.

Свойство 3. Вероятность случайного события есть положительное число, заключенное

между нулем и единицей.

Доказательство. Случайное событие происходит при некоторых исходах опыта, но не при

всех, следовательно, 0 < m < n, и из (1.1) следует, что 0 < p(A) < 1.

Определение 1.9. Статистической вероятностью события считают его относительную

частоту или число, близкое к ней.

Замечание 1. Из формулы (1.2) следует, что свойства вероятности, доказанные для ее

классического определения, справедливы и для статистического определения вероят-

ности.

Замечание 2. Для существования статистической вероятности события А требуется: 1) возможность производить неограниченное число испытаний;