1)Уравнения электромагнитного поля

Эл.маг. поле в любой среде в каждый момент времени определяется 4-мя векторами : Е и D - характ. электрическое поле, и Н и В - хар. магн. поле.

Уравнения Максвелла.

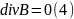
где -плотность электрических зарядов -плотность токов проводимости

Они характеризуют источник поля, наличие которых приводит к его возбуждению в окружающем пространстве.Число уравнений мень­ше числа неизвестных поэтому добавим линейную форму записи материальных урав. (5)

где , , абсолютные диэлектрическая, магнитная проницаемости среды и удельная элек. проводим. Величины , , - электрофизические параметрами среды. В случае произвольных полей и сред величины , , - тензоры, матричные элементы которых зависят от Е , Н и t. Выделяют линейные среды(параметры которых не зависят от E и H полей) и нелинейные среды (в которых эта зависимость наблюдается. (в сильных полях)) Среду называют однородной, если ее параметры не зависят от координат, и неоднородной, если такая зависим. есть. Изотропные среды - Е и D, и Н и В параллельны при любой ориентации э/м поля (характер э/м процессов в таких средах не зависит от направления векторов Е и Н)анизотропными - векторы Е и D, и (или) Н и В не параллельны (в монокрис­таллах).пространственной и временной дисперсией - формулы (5) предполагают, что значения векторов D и В в точке зависят только от значений Е и Н в той же координате и в тоже врем, реально их значения могут зависеть от Е и Н в соседних точках и в более ранние моменты времени.

Комплексная форма записи

Большое значение имеют э/м колебания изменяющееся по sin(гармонич.) закону. (Иначе раскладываем в ряд или интеграл Фурье.)

связь комплексных урав. с первонач.- оператор заменяем .

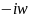Уравнения Максвелла в этом случае примут следующий вид:

Комплексная диэл. прониц. вещества:

Здесь действительная часть описывает интенсивность процесса поляризации, а мнимая учитывает плотность токов проводимости.

Также вводится и комплексная магнитная проницаемость :

Где и - углы электрических и магнитных потерь. Исходя из всего выше сказанного

уравнения э/м поля для гармонических процессов:

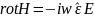
2)Сторонние токи

Сторонние токи – токи которые определяются внешними источниками и не зависят от создаваемых ими э/м поля. Рассмотрим данный процесс на примере: Эл. токи не только возбуждают поле, но и сами возникают под его воздействием на среду. Например передающая антенна излучает э/м волны в пространство здесь мы имеем два вида токов токи в антенне - первичные источники поля ; токи в среде - возникающие под действием э/м поля. Те токи что в среде возбуждают свое э/м поле, но являются лишь вторичными источниками, возбуждаемыми самим полем. В результате получим что записанное уравнение не учитывает наш первичный источник э/м поля поэтому мы и вводим такое понятие как сторонние токи.

С учетом сторонних токов наше уравнение примет вид:

уравнения э/м поля для гармонических процессов с учетом сторон.токов:

Граничные условия

Комплексные диэл. и магнит. проницаемость могут произвольным образом меняться в пространстве, а на границе раздела двух сред могут иметь скачок.

Рассмотри 2 случая:

1)Две поверхности перпендик.

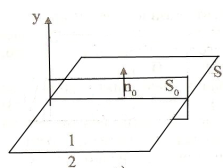
В рассматриваемом случае мы может говорить о наличии тока, протекающего в бесконечно тонком слое вблизи поверхности раздела сред. Этот ток называют плотностью поверхностного тока . Для него справедливо соотношение:

где под - сумма как стороннего, так и возбужденного полем тока.

Это равенство означает, что разность между касательными составляющими вектора Н на границе раздела двух сред численно равна плотности поверхностного тока. Если то составляющие непрерывны .

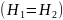Тоже получим и для т.е. касательная составляющая вектора Е всегда непрерывна на поверхности раздела двух сред.

- нормаль к поверхности

2) Рассмотрим параллелепипед с гранями

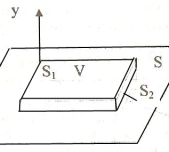
Для этого случая справедливо:

А также

- нормаль к поверхности