[Править]Формула преобразования скоростей

Достаточно продифференцировать   в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор  ,

где радиус-вектор какого-то тела A в системе отсчета K обозначим за  , а в системе отсчета K' — за  ,

подразумевая, как всегда в классической механике, что время   в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:  .

Тогда в любой момент времени

и в частности, учитывая

,

имеем:

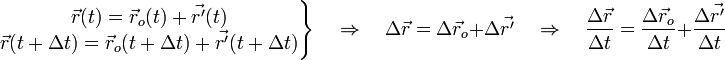
где:

 — средняя скорость тела A относительно системы K;

 — средняя скорость тела А относительно системы K' ;

 — средняя скорость системы K' относительно системы K.

Если   то средние скорости совпадают с мгновенными:

или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

Инвариантность законов классической механики при переходе в движущуюся ИСО подразумевает в том числе и то, что ускорения, вызванные взаимодействием любых двух материальных точек должны быть направлены по прямой, соединяющей точки, противоположно друг другу. Этому требованию удовлетворяют преобразования Галилея. Если в неподвижной ИСО ускорения, вызванные взаимодействием двух материальных точек, направлены по прямой, соединяющей точки, противоположно друг другу, то при переходе в движущуюся ИСО по Лоренцу, эти ускорения преобразуются так, что уже не будут направлены по прямой соединяющей точки.  Преобразования Лоренца не оставляют инвариантным направление ускорений, вызванных взаимодействием любых двух материальных точек. Классический закон преобразования такой  .

8 Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы.Часто систему материальных точек называют механической системой.Действующие на точки механической системы активные силы и реакции связей можно разделить на внешние и внутренние силы. Внутренними силами называют силы взаимодействия между материальными точками одной механической системы. Внешние силы - это силы взаимодействия точек данной механической системы с точками какой-либо другой системы.

Закон сохранения импульса системы точек выводится из второго закона Ньютона. Сначала записываем формулу второго закона для каждой точки системы, а затем полученные равенства складываем так, что слева получается производная по времени от вектора импульса системы точек, а справа - сумма всех действующих сил. Но по третьему закону Ньютона сумма сил, действующих между каждой парой точек, равна нулю, поэтому справа остается только сумма внешних сил.

 закон сохранения импульса системы материальных точек: общий момент импульса системы относительно какой-либо неподвижной оси остается постоянным, если момент внешних сил относительно этой оси равен нулю

9