Пример 1.17

Дано

R₁ = 1 Ом; R₂ = 2 Ом; R₃ = 3 Ом; R₄ = 4 Ом; R₅ = 0,6 Ом; R₆ = 3 Ом; J = 1 А; Е₅ = 1 В.

Определить

токи во всех ветвях методом контурных токов для схемы на рис.1.17.1; проверить баланс мощностей.

Решение

Полагаем, что источник тока J обладает бесконечно большим внутренним сопротивлением R_вн = . Тогда, система уравнений в матричном виде запишется как:

.

Раскрытие главного определителя дает:

.

Замена коэффициентов первого и второго столбцов главного определителя значениями свободными параметрами даст:

; .

Находим численные значения контурных токов I_K1 = I₁ и I_K2 = I₂:

; .

Ток I₃ и ток I₅ диагонали соответственно равны:

;

.

Баланс мощностей:

.

Предварительно найдем падение напряжения между узлами А и В:

.

Тогда

;

.

Пример 1.18

Д ано

R₁ = 30 Ом; R₂ = 20 Ом; R₃ = 20 Ом; R₄ = 40 Ом; R₅ = 60 Ом; R₆ = 40 Ом; R₇ = 10 Ом; J₇ = 0.4 А; Е₃ = 3 В;

Е₄ = 4 В; Е₆ = 18 В.

Определить

токи во всех ветвях, используя метод контурных токов для схемы на рис.1.18.1; составить и рассчитать баланс мощностей.

Решение

В матричной форме система уравнений будет иметь вид:

.

Раскроем главный определитель:

.

Замена первого столбца главного определителя, матрицей-столбцом свободных параметров дает:

.

Тогда контурный ток I_K1 будет равен:

.

Выполнив аналогичные действия, найдем контурные токи I_K4 и I_K6:

; .

; .

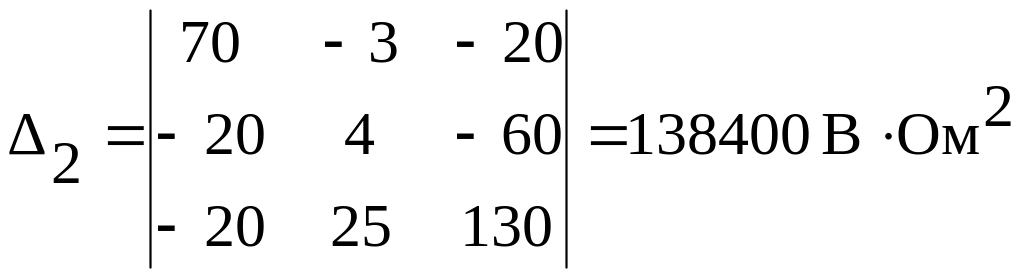Остальные неизвестные токи найдем, исходя из первого закона Кирхгофа:

Баланс мощностей

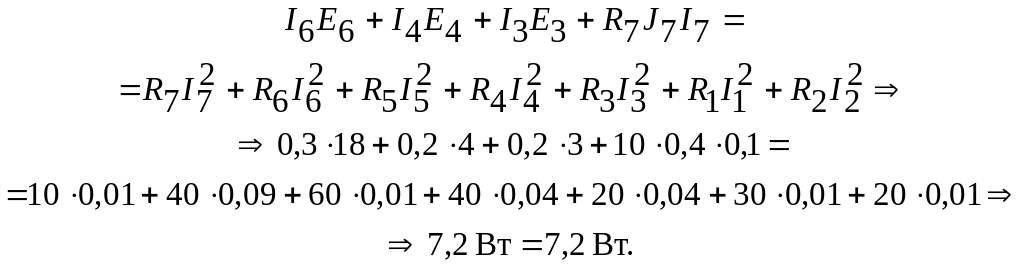
1.19

Д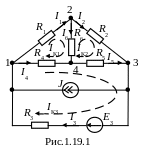 ано

R₁ = 20 Ом; R₂ = 30 Ом; R₃ = 40 Ом;

R₄ = 80 Ом; R₅ = 20 Ом; R₆ = 20 Ом;

Е₃ = 16 B; J = 0,3 А.

Определить

токи во всех ветвях, для схемы на рис.1.19.1, воспользовавшись методом контурных токов. Выполнить проверку расчета.

Решение

В матричной форме система уравнений будет иметь вид:

.

Подстановка численных значений коэффициентов и последующее раскрытие главного определителя дает:

Заменив первый столбец главного определителя, матрицейстолбцом свободных параметров, получим:

Тогда контурный ток I_К1 определится как:

По аналогии для контурных токов I_К2 и I_К3:

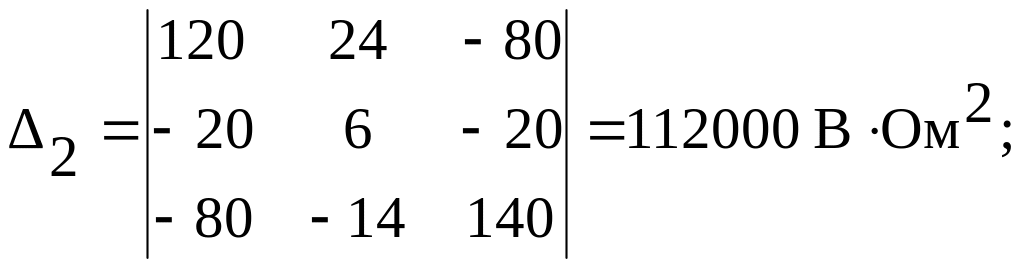
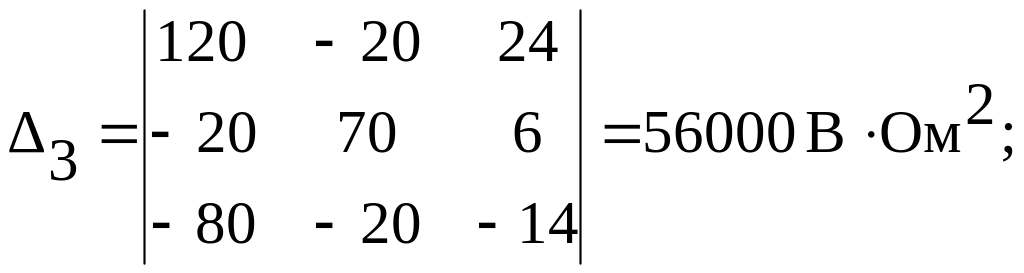
Остальные неизвестные токи найдем, исходя из первого закона Кирхгофа:

Проверка

Для проверки выполненных вычислений воспользуемся вторым законом Кирхгофа , обходя замкнутый контур 1,2,3,4,1:

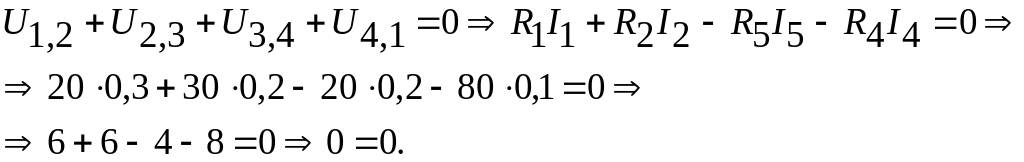
Метод (принцип) наложения

Этот метод вытекает из уравнений электрического состояния цепей с линейными элементами.

При действии нескольких источников напряжения или токов в линейной электрической схеме токи в ее ветвях находят алгебраическим суммированием токов от каждого источника в отдельности. При этом неучтенные источники заменяют их внутренними сопротивлениями, закорачивая источники э.д.с. и размыкая источники тока.

Пример 1.20

В схеме рис.1.20.1 найти токи методом наложения.

Решение

Находим токи в ветвях схемы при действии источника э.д.с Е, без учета источника тока J, полагая, что R_вн = :

Находим токи в ветвях схемы при действии источника тока J, полагая, что Е = 0:

Зададим положительное направление токов в ветвях исходной схемы и найдем их величины, алгебраически суммируя значения частичных токов:

.

Если искомый ток в схеме получится со знаком минус, то его действительное значение не совпадает с выбранным направлением тока.

Метод наложения можно применять для нахождения любых физических величин, которые связаны между собой линейной зависимостью. Исключение накладывается на вычисление мощностей, поскольку мощность  функция квадратичная.