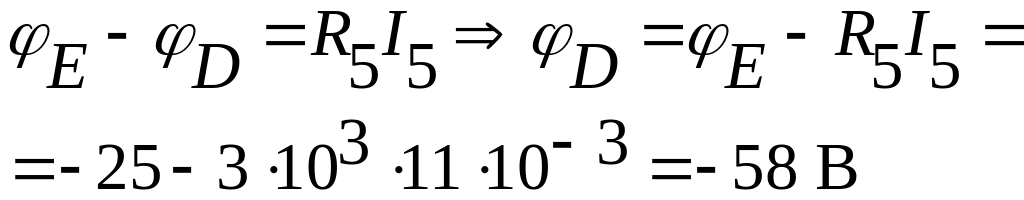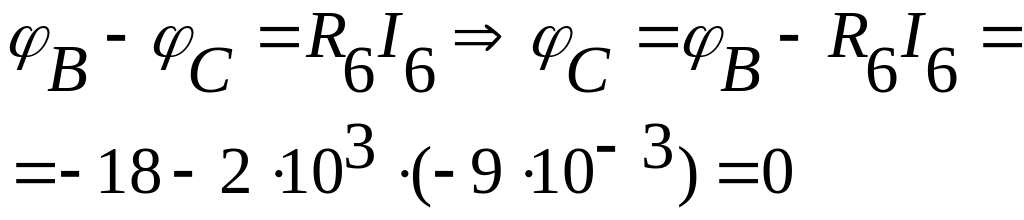Пример 1.8

Р ис.1.8.1

Дано:

E₁ = 20 В; E₂ = 50 B; E₃ = 20 B; E₄ = 30 B; R₁ = 1 Ом; R₂ = 2 Ом; R₃ = 3 Ом; R₄ = 4 Ом.

Определить

силу тока I; потенциалы точек 1÷9; построить потенциальную диаграмму.

Решение

Для схемы на рис.1.8.1 можно записать:

Примем потенциал точки 1 равным нулю ( ), тогда:

	(потенциал точки 2).
	(потенциал точки 3).
	(потенциал точки 4).
	(потенциал точки 5).
	(потенциал точки 6).
	(потенциал точки 7).
	(потенциал точки 8).
	(потенциал точки 9).

По вычисленным потенциалам точек 0÷9, строим потенциальную диаграмму или график распределения потенциала вдоль цепи (рис.1.8.2).

Ток, через любой пассивный элемент цепи, равен отношению напряжения к сопротивлению рассматриваемого участка цепи. Это отношение будет соответствовать тангенсу угла наклона прямых, определяющих изменение потенциала, к оси абсцисс. Но поскольку ток в данной схеме остается неизменным, то и наклон прямых одинаков.

Р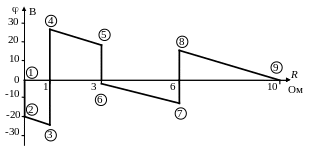 ис.1.8.2

Пример 1.9

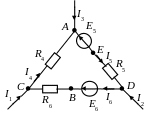
Рис.1.9.1

Дано I1 = 10 мА; I2 = 20 мА; R4 = 5 кОм; E5 = 20 B; R5 = 3 кОм; E6 = 40 B; R6 = 2 кОм. Определить токи I3÷I6. Для нахождения токов I4÷I6 составить систему уравнений в матричной форме и вычислить соответствующие определители. Построить потенциальную диаграмму. Оценить мощность потребителей (приемников) и источников электрической энергии.

Решение

Согласно схеме на рис.1.9.1, величину тока I₃ можем найти сразу:

Для нахождения величин остальных токов, запишем систему уравнений, составленную по законам Кирхгофа:

В матричной форме система уравнений приобретает вид:

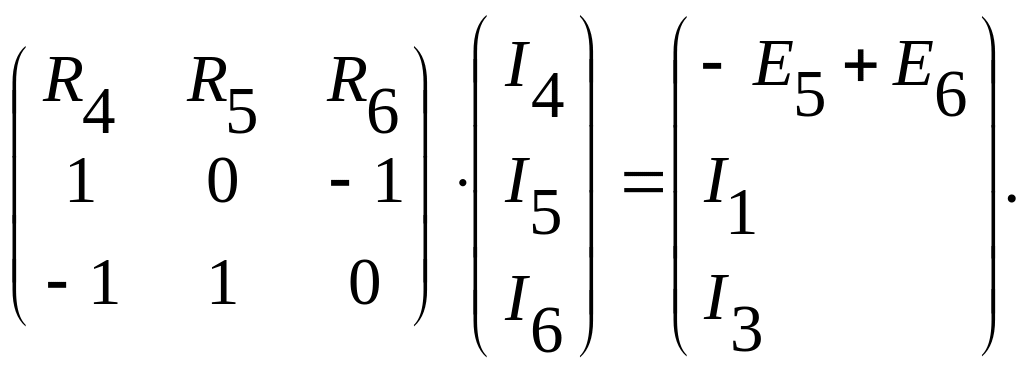
Раскрыв главный определитель коэффициентов при неизвестных, получим:

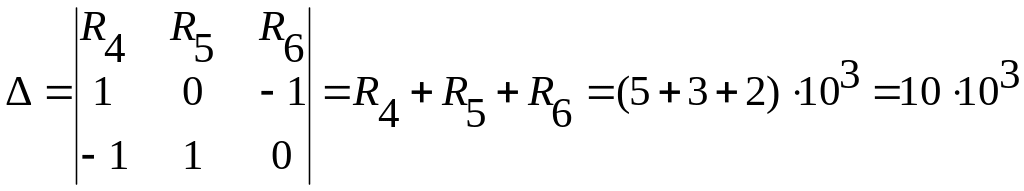Ом.

Произведя замену коэффициентов первого столбца главного определителя, столбцом свободных параметров получим:

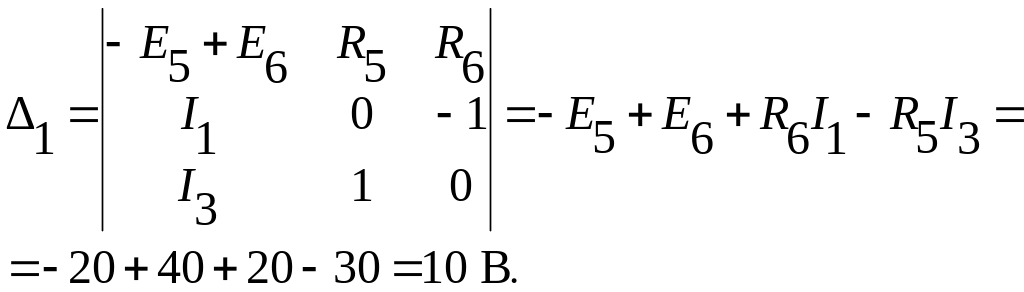
Ток I₄ будет равен:

.

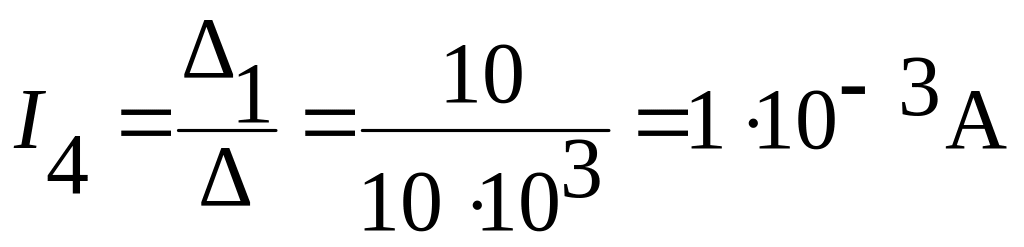Произведя замену коэффициентов второго столбца главного определителя, столбцом свободных параметров получим:

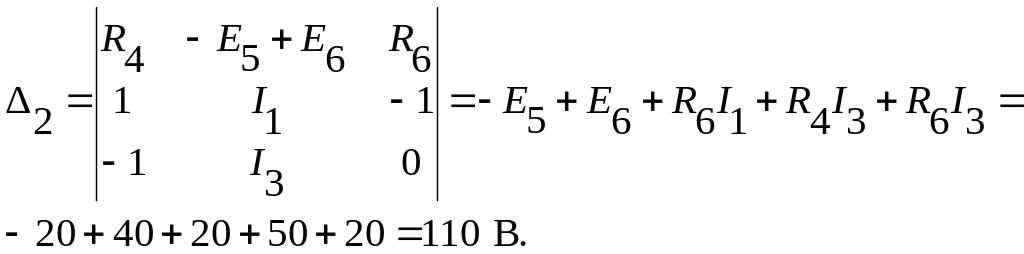
Тогда ток I₅ будет равен:

.

Заменив коэффициенты третьего столбца главного определителя, столбцом свободных параметров запишем:

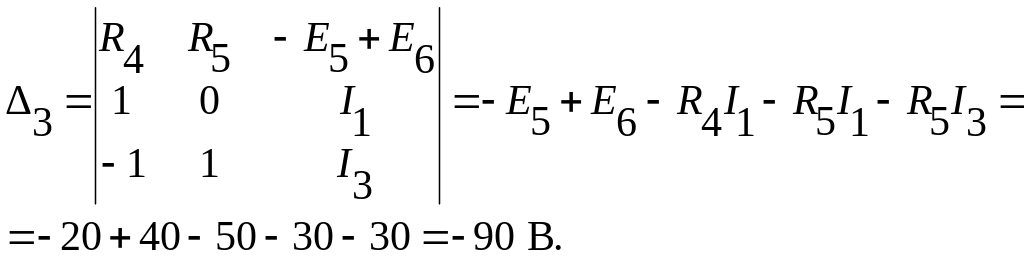
Найдем величину тока I₆:

.

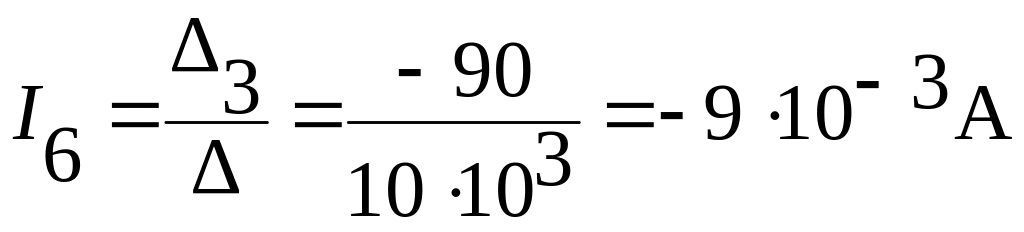Можно убедиться в том, что для любого узла схемы (рис.1.9.1), сумма токов равна нулю.

Примем потенциал точки С равным нулю, тогда:

	(потенциал точки A).
	(потенциал точки E).
	(потенциал точки D).
	(потенциал точки B).
	(потенциал точки C).

Обходя замкнутый контур (CAEDBC), построим потенциальную диаграмму (рис.1.9.2).

Из приведенных вычислений следует, что направление токов I₂, I₆ противоположно указанным на схеме (рис.1.9.1), поэтому источники E₅, E₆ являются потребителями энергии (приемниками). Следовательно, мощность, потребляемая всеми элементами схемы, будет равна:

Р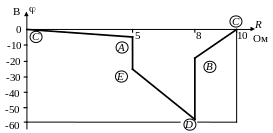 ис.1.9.2

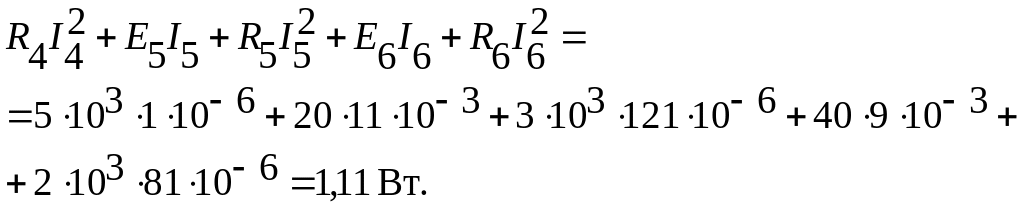
Пусть, например, токи I₁, I₂, I₃ обусловлены наличием сторонних источников э.д.с., энергия которых, через упомянутые токи, подводится к схеме.

Тогда электрическая цепь со сторонними источниками э.д.с. Е₁ и Е₃ и с измененными направлениями токов I₂ и I₆ будет иметь вид, показанный на рис.1.9.3.

Р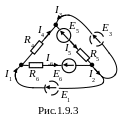 ассчитаем величины сторонних источников E₁ и E₃. Согласно рис. 1.9.3. эти величины найдем из соотношений:

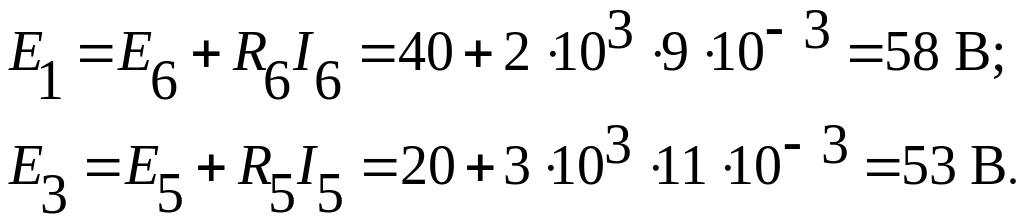
Суммарная мощность этих источников:

Таким образом, мощность, генерируемая сторонними источниками E₁ и E₃ равна мощности потребляемой всеми элементами схемы рис. 1.9.1.