Пример 1.39 Дано

В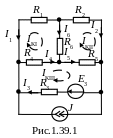 етви электрической цепи на рис.1.39.1 содержат активные сопротивления, источники э.д.с. и тока.

Определить

систему уравнений для контурных токов, исходя из матрицы сопротивлений ветвей, контурной матрицы, матрицы контурных сопротивлений, матриц источников э.д.с. и тока.

Решение

Составим и заполним таблицу, предварительно задав направление обхода каждого из контуров.

		ветви
		1	2	3	4	5	6
контуры	I	+1	0	0	–1	0	+1
	II	0	+1	0	0	–1	–1
	III	0	0	+1	+1	+1	0

Согласно таблице запишем контурную матрицу:

.

Матрица сопротивлений ветвей будет диагональной:

.

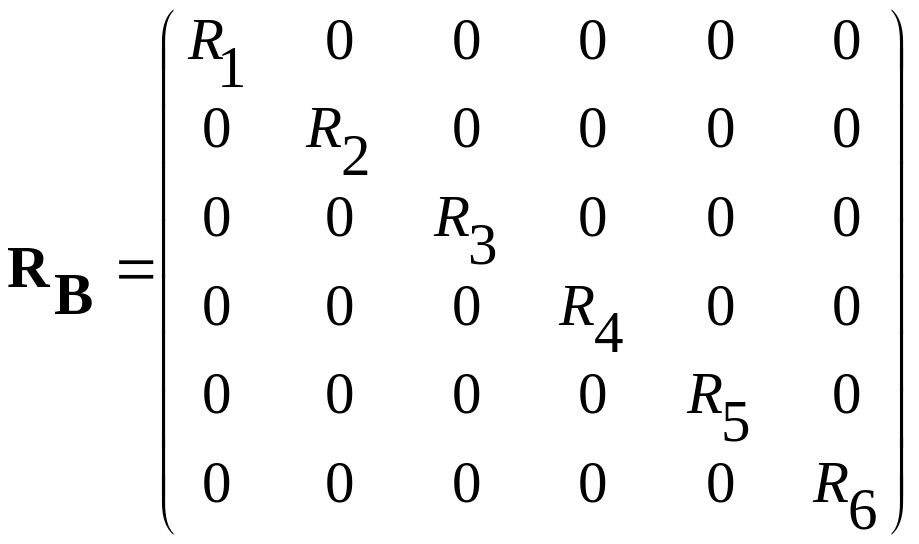Находим произведение матрицы сопротивлений ветвей R_B и транспонированной контурной матрицы В^Т:

= .

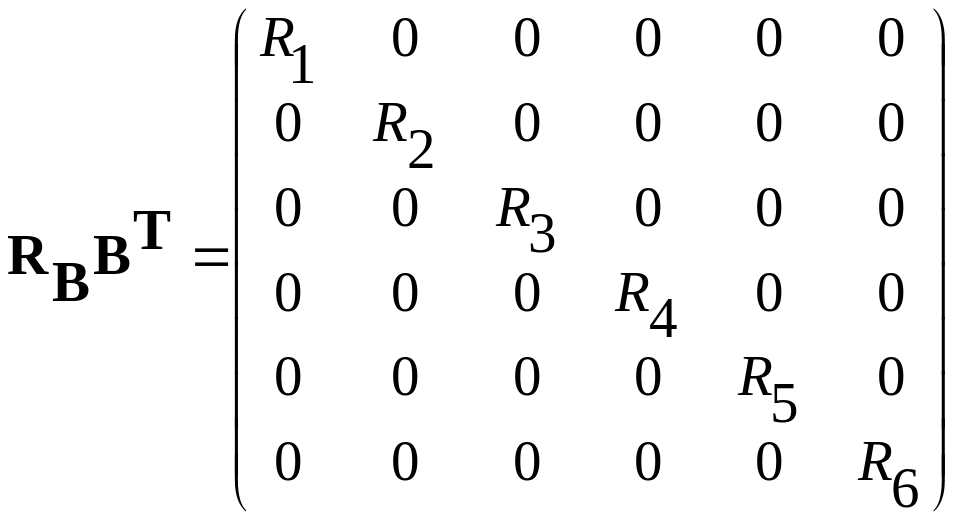
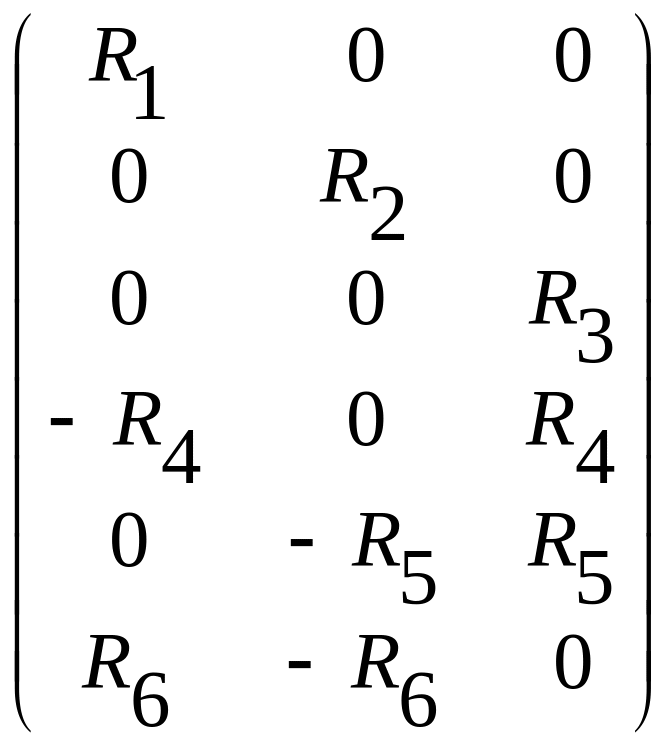Находим матрицу контурных сопротивлений:

.

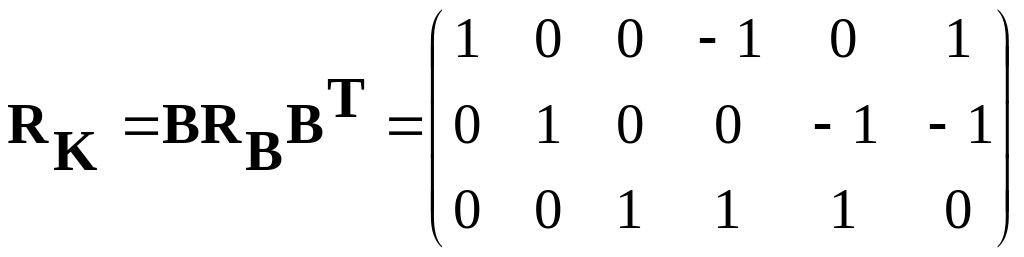
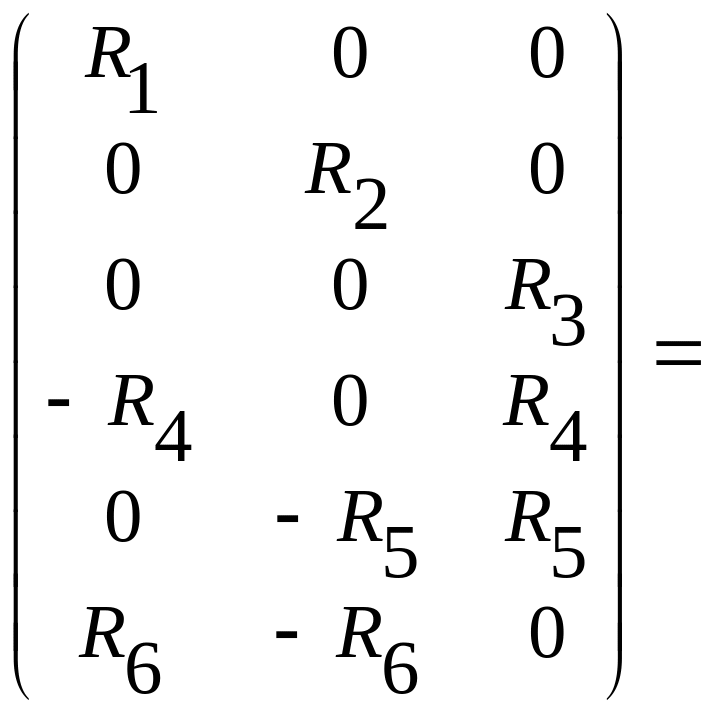
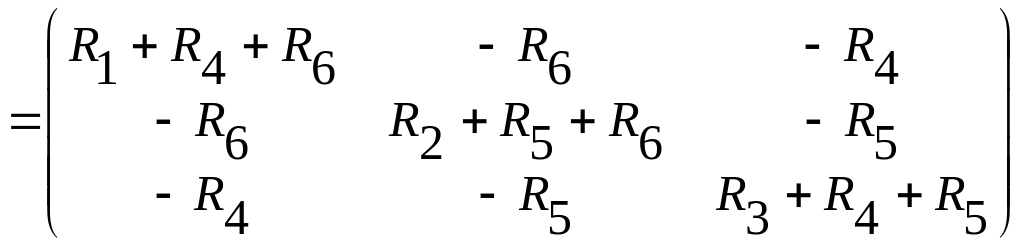Организуем столбцовые матрицы контурных токов ветвей, источников э.д.с. и источников тока:

; ; .

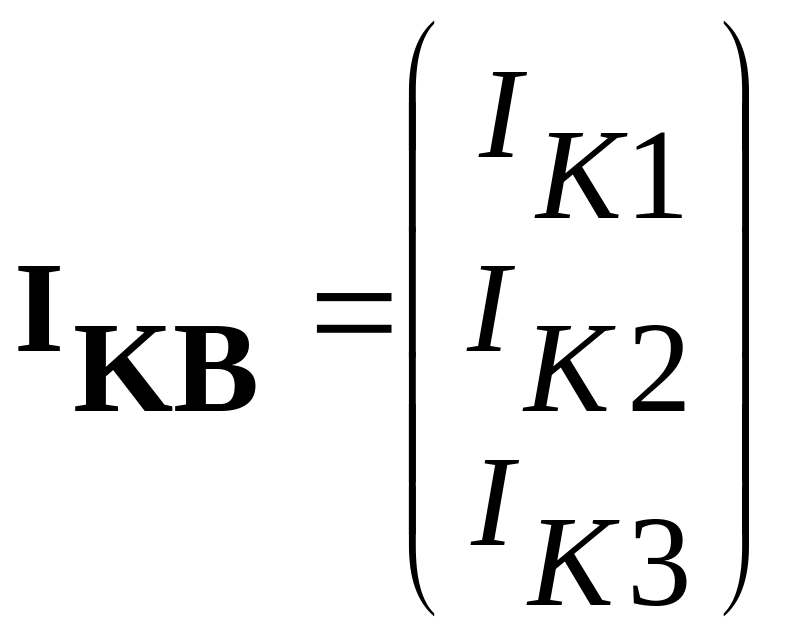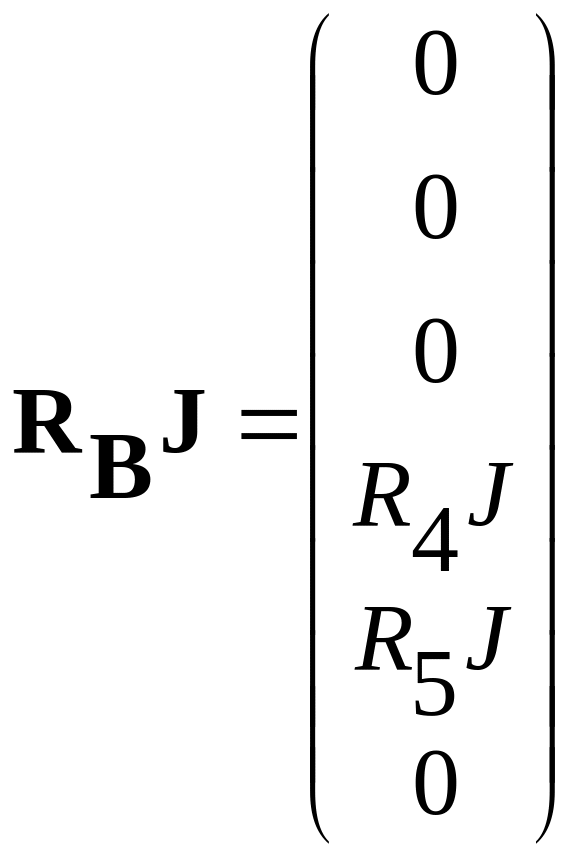Тогда матричное уравнение приобретает известный вид:

.

Или с учетом выше организованных матриц:

=

=  .

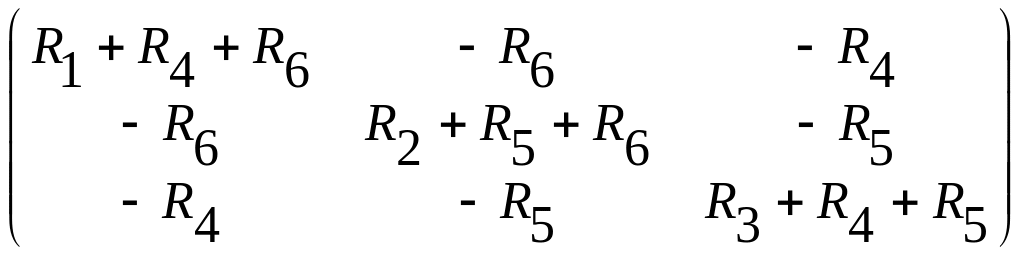
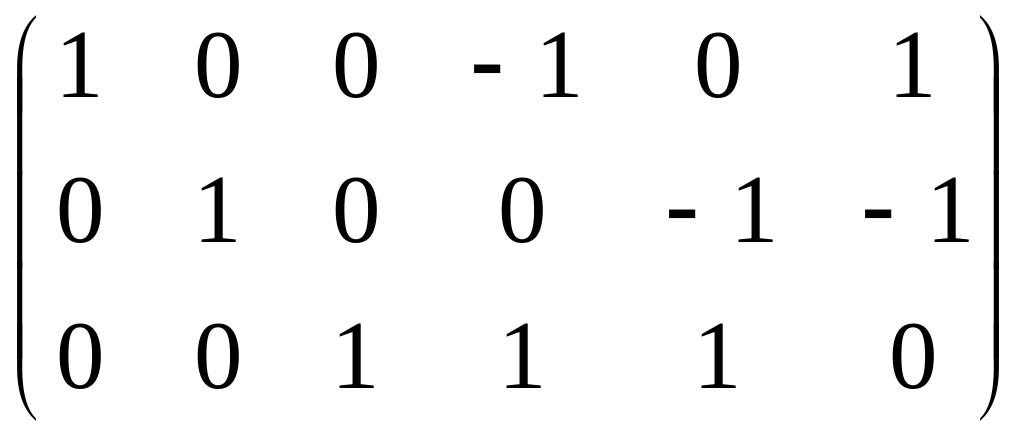
Произведя соответствующие действия над матрицами левой и правой частей последнего уравнения, получим искомую систему в контурных токах:

Токи в ветвях, выраженные через контурные токи, легко найти, воспользовавшись уравнением:

,

или

= ,

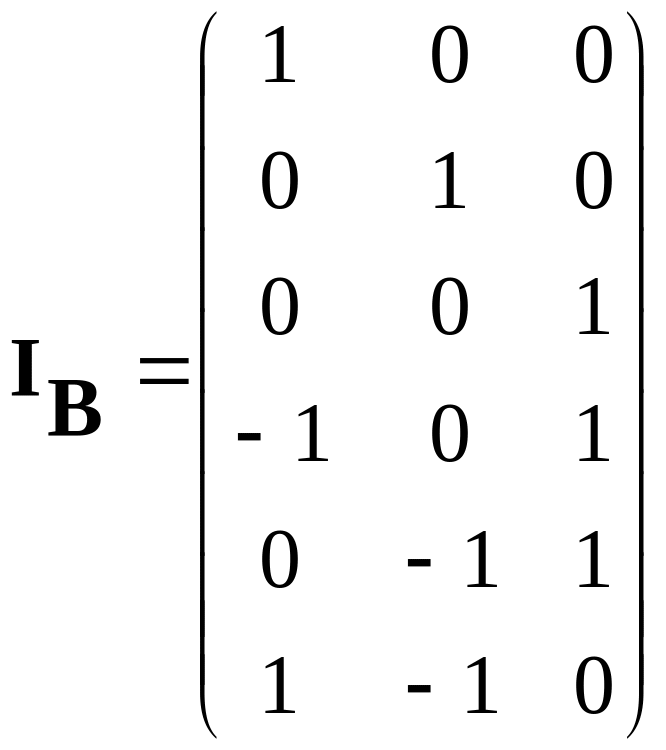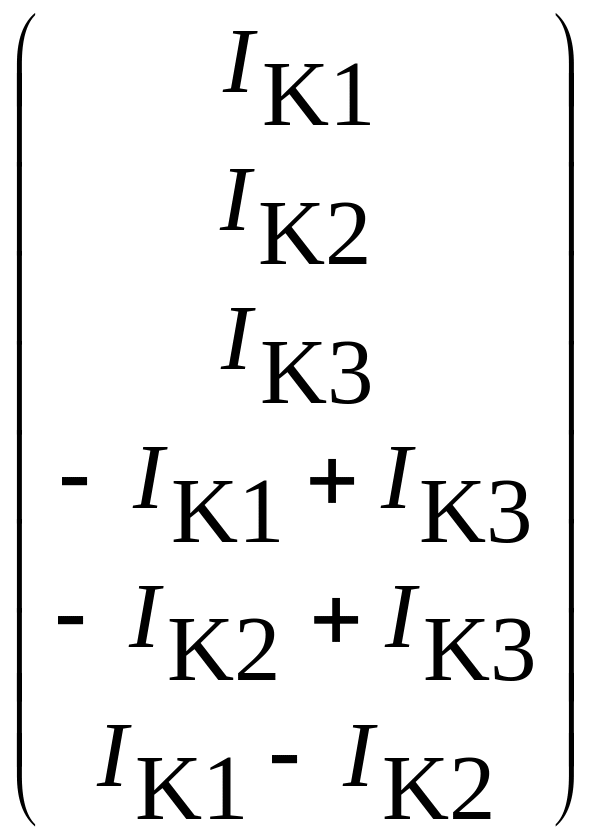где ; ; ; ; ; .

Пример 1.40

Дано

На рис.1.40.1 изображен сигнальный (направленный) граф. Сигнальные графы это совокупность узлов, представляющих зависимые и независимые переменные системы уравнений и соединяющих их ветвей со стрелками и передачами, указывающими связи между переменными.

О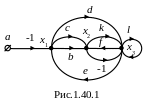 пределить

систему уравнений по заданному графу.

Решение

Граф, представленный на рис.1.40.1 включает в себя узел а – исток, петлю l и три смешанных узла х₁, х₂, х₃, для которых запишем соответствующие сигналы для каждого узла, с учетом того, что сигнал в узле равен сумме сигналов, подходящих к данному узлу:

; ; .

Таким образом, граф соответствует следующей системе уравнений:

Пример 1.41

Д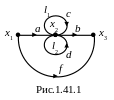 ано

Задан сигнальный граф (рис.1.41.1).

Определить

коэффициент передачи сигнала графа из первого узла в третий, т.е. найти отношение х₃/х₁:

1) посредством передачи сигналов графа;

2) посредством правил преобразования графа, путем последовательного упрощения его структуры;

3) применением формулы Мезона.

Решение

1) Запишем уравнения сигналов для соответствующих узлов графа:

Тогда система уравнений графа:

Из второго уравнения системы имеем:

Подставив правую часть последнего равенства в первое уравнение системы, получим:

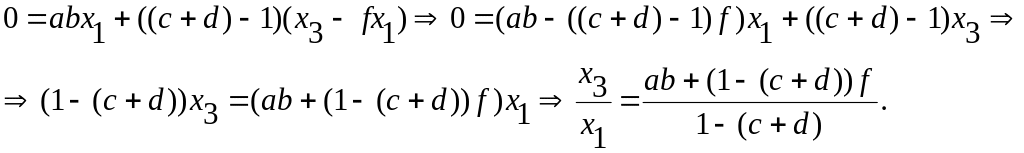
2) Приведем структуру графа (рис.1.41.1) к более простому виду, заменой двух петель одной на рис.1.41.2. Уравнения узловых сигналов упрощенного графа:

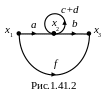
Структуру графа на рис.1.41.2, за счет устранения петли, приводим к виду представленному на рис.1.41.3.

Уравнение узлового сигнала упрощенного графа:

Н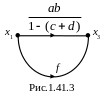 аконец, осуществив преобразование двух параллельно соединенных однонаправленных ветвей рис.1.41.3, получим граф, не подлежащий дальнейшему упрощению рис.1.41.4. Уравнение узлового сигнала упрощенного графа:

И з последнего уравнения следует:

3) Формула Мезона позволяет определить коэффициент передачи сигнала, исходя из путей графа (непрерывная последовательность ветвей сигнального графа) и его контуров (замкнутый путь графа):

Граф (рис.1.41.1) имеет два прямых пути от узла х₁ к узлу х₃: Р₁ = ab и Р₂ = f, а также два контура обратной связи: l₁ = c и l₂ = d. Первый путь Р₁ походит через все узлы графа, следовательно:

Определитель ₂ получим вычитанием из единицы суммы двух контуров l₁ и l₂, несоприкасающихся со вторым путем Р₂:

Определитель  получим вычитанием из единицы передач всех контуров (передача контура – произведение передач ветвей в данном контуре). В нашем случае это передачи двух контуров:

Таким образом, коэффициент передачи сигнала графа:

Итак, во всех трех рассмотренных случаях результат получился один и тот же.