Пример 1.34

Дано

Известна полная узловая матрица А_П

.

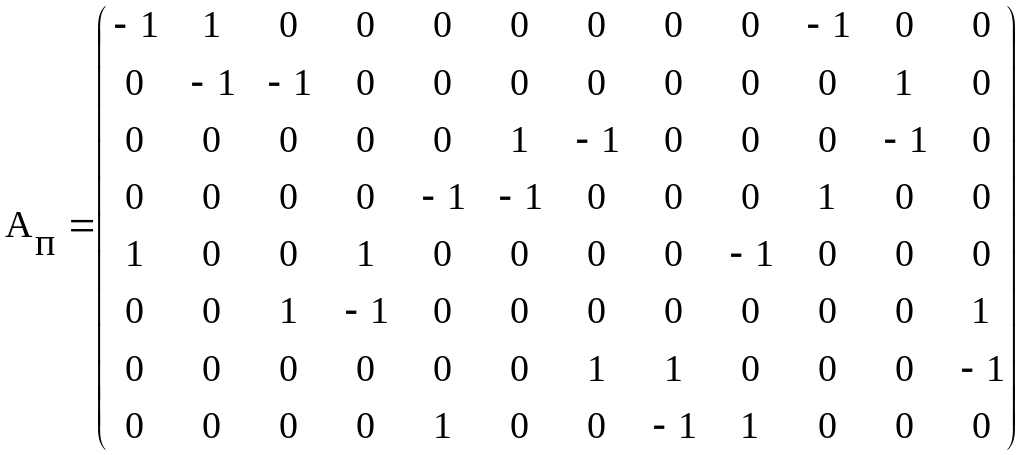Определить

по известной полной узловой матрице А_П направленный граф электрической цепи.

Решение

Полная узловая матрица А_П включает в себя двенадцать столбцов и восемь строк. Следовательно, граф электрической цепи содержит двенадцать ветвей и восемь узлов.

Из матрицы А_П следует:

- ветвь 1 связывает узлы 5 и 1;

- ветвь 2 связывает узлы 1 и 2;

- ветвь 3 связывает узлы 6 и 2;

- ветвь 4 связывает узлы 5 и 6.

Таким образом, ветви 1, 2, 3, 4 образуют замкнутый контур с узлами 5, 1, 2, 6. Далее

- ветвь 5 связывает узлы 8 и 4;

- ветвь 6 связывает узлы 3 и 4;

- ветвь 7 связывает узлы 7 и 3;

- ветвь 8 связывает узлы 7 и 8.

Таким образом, ветви 5, 6, 7, 8 образуют второй замкнутый контур с узлами 8, 4, 3, 7. Наконец

- ветвь 9 связывает узлы 8 и 5;

- ветвь 10 связывает узлы 4 и 1;

- ветвь 11 связывает узлы 2 и 3;

- ветвь 12 связывает узлы 6 и 7.

С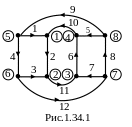 ледовательно, ветви 9, 10, 11, 12 связывают соответствующие узлы первого и второго контуров. Ориентация ветвей определяется согласно выше сформулированным правилам. Строим направленный граф (рис.1.34.1). Возможны и другие варианты рассуждений в построении графа.

П ример 1.35

Дано

Задан граф на рис. 1.35.1.

Определить

матрицу узловых проводимостей.

Решение

Составим узловую матрицу для заданного графа с базисным узлом (0).

.

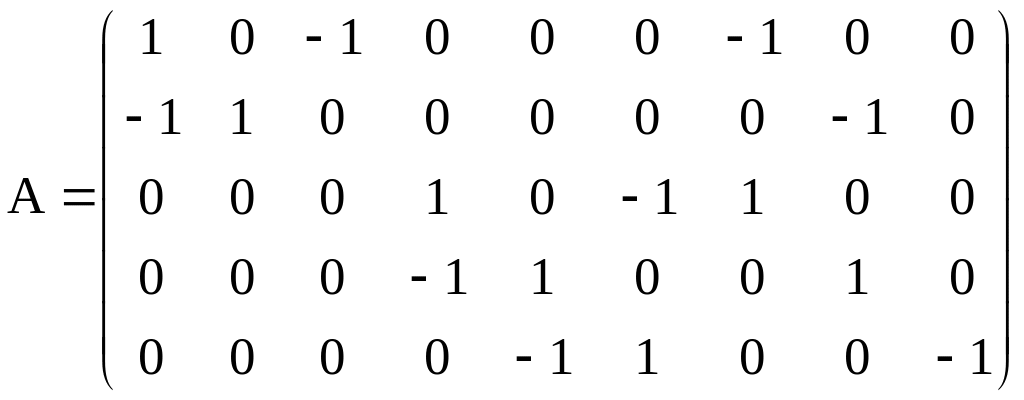При отсутствии индуктивных взаимных связей между ветвями, матрица проводимости ветвей будет диагональной:

,

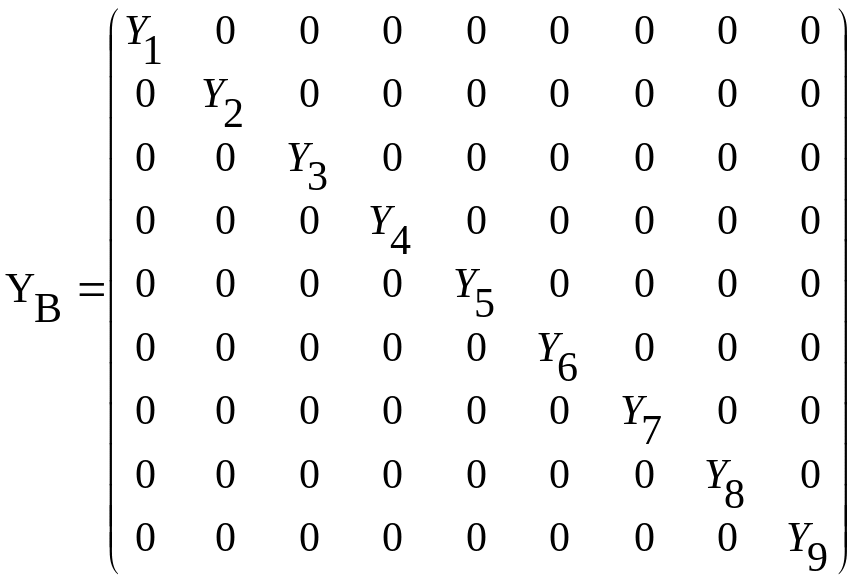где Y₁,…, Y₉ – собственные проводимости ветвей, в состав которых могут входить активные и реактивные линейные сопротивления. Матрица проводимостей (обратная матрице сопротивлений) всегда квадратная, а порядок ее равен числу ветвей.

Находим произведение матрицы проводимости ветвей Y_В и транспонированной узловой матрицы А^Т:

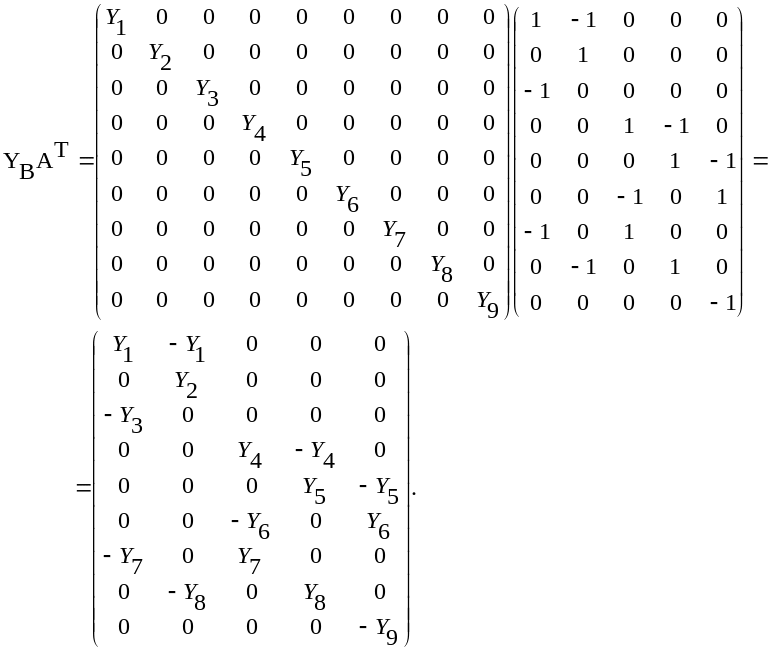
После того как найдено произведение матрицы проводимости ветвей и транспонированной узловой матрицы можем записать матрицу узловых проводимостей:

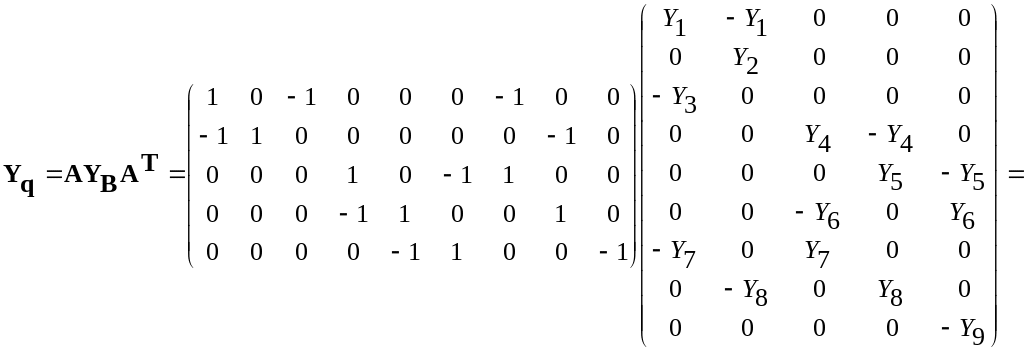
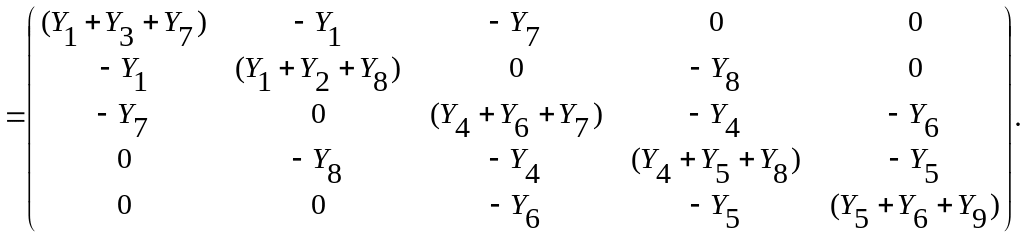
Таким образом, тройное матричное произведение АY_ВА^Т определяет матрицу узловых проводимостей Y_q.

Пример 1.36

Д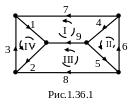 ано

Задан направленный граф некоторой электрической цепи на рис.1.36.1.

Определить

контурную матрицу.

Решение

Выберем направление обхода каждого простого контура, т.е. такого контура, внутреннюю область которого не пересекает ни одна ветвь. Составим таблицу таким образом, чтобы число строк равнялось числу независимых контуров, а число столбцов равнялось числу ветвей графа, причем:

- если направление обхода контура совпадает с направлением ветви этого контура, то в клетку пересечения их нумераций вписывается положительная единица;

- если направление обхода контура не совпадает с направлением ветви этого контура, то в клетку пересечения их нумераций вписывается отрицательная единица;

- если ветвь не входит в контур, то в клетку пересечения их нумераций вписывается ноль.

Тогда

		ветви
		1	2	3	4	5	6	7	8	9
контуры	I	+1	0	0	-1	0	0	1	-1	0
	II	0	0	0	1	1	1	0	0	0
	III	0	1	0	0	-1	0	0	1	-1
	IV	-1	-1	-1	0	0	0	0	0	0

Согласно заполненной таблице запишем контурную матрицу:

.
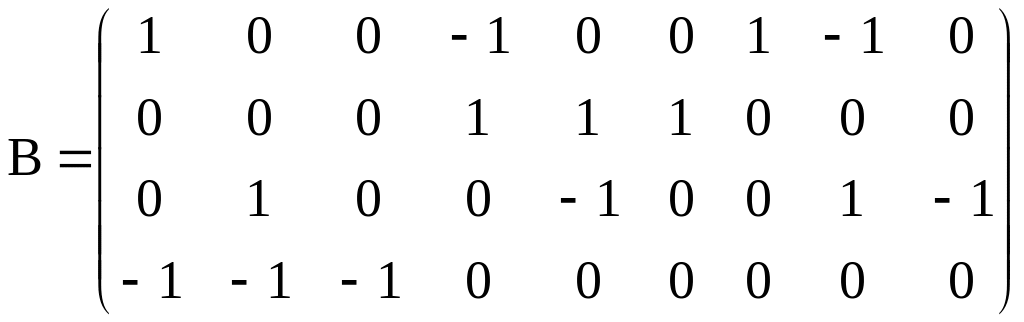