Формулы для расчета термодинамических процессов

Процесс и уравнение процесса	Соотношение между параметрами	Работа, Дж / кг; Дж / моль	Изменение внутренней энергии, Дж / кг; Дж / моль	Теплота, Дж / кг; Дж / моль	Изменение энтропии, Дж / (кг · К); Дж / (моль · К)
1	2	3	4	5	6
1. Изохорный υ = const		l = 0	Δu = cυm ∙ (T2 – T1)	q = cυm (T2 – T1)	Δs = cυm ln
2. Изобарный р = сonst		l = p (υ2 – υ1); l = R (T2 – T1)	Δu = cυm (T2 – T1)	q = cpm (T2 – T1)	Δs = cpm ln
3. Изотермический Т = const; pυ = const		l = R T ln ; l = R T ln ; l = p1 υ1 ln .	Δu = 0	q = l	Δs = R ln ; Δs = R ln ; Δs = ln

Окончание табл. 6

Процесс и уравнение процесса	Соотношение между параметрами	Работа, Дж / кг; Дж / моль	Изменение внутренней энергии, Дж / кг; Дж / моль	Теплота, Дж / кг; Дж / моль	Изменение энтропии, Дж / (кг · К); Дж / (моль · К)
1	2	3	4	5	6
4. Адиабатный рυk = const, где k = – показатель адиабаты	; = ; =	l = (p1 υ1 – p2 υ2); l = (T1 – T2); l = ; l =	Δu = cυm (T2 – T1)	q = 0	Δs = 0
5. Политропный рυn = const, где n = – показатель политропы	; = ; =	l =	Δu = cυm (T2 – T1)	q = cυm	Δs = cυm

Теплота, подведенная в изохорном процессе 2 – 3 рассчитывается по формуле (табл. 6):

q′₁ = c_υm (T₃ – T₂). (20)

Теплота, подведенная в изобарном процессе 3 – 4:

q″₁ = c_pm (T₄ – T₃). (21)

Суммарная подведенная теплота в цикле:

q₁ = q′₁ + q″₁. (22)

Отведенная теплота в изохорном процессе 5 – 1:

q₂ = c_υm (T₅ – T₁). (23)

Примечание: В расчетах значения c_υm и c_pm принимаются равными и соответственно (см. п. 2.2).

Подставляя (20), (21) и (23) в (19) получаем:

. (24)

Известно, что показатель адиабаты . Следовательно, с_рm = k с_υm. Подставляя это выражение в (24) получаем:

. (25)

Выразим температуры всех точек через температуру точки 1.

Для адиабатного процесса 1 – 2 с учетом, что имеем (табл. 7):

= ; откуда

Т₂ = Т₁ = Т₁ · ε^k–1. (26)

Для изохорного процесса 2 – 3 с учетом и выражения (26) имеем:

, откуда

Т₃ = Т₂ · λ = Т₁ · ε^k–1 · λ. (27)

Для изобарного процесса 3 – 4 с учетом табл. 7, характеристики цикла и формулы (27) имеем:

, откуда

Т₄ = Т₃ · ρ = Т₁ · ε^k–1 · λ · ρ. (28)

Для адиабатного процесса 4 – 5 с учетом табл. 7 имеем:

. (29)

Рассмотрим дробь, стоящую в правой части (29): υ₅ = υ₁, так как процесс 1 – 5 изохорный.

Если полученную дробь умножим и разделим на ( ), и будем иметь:

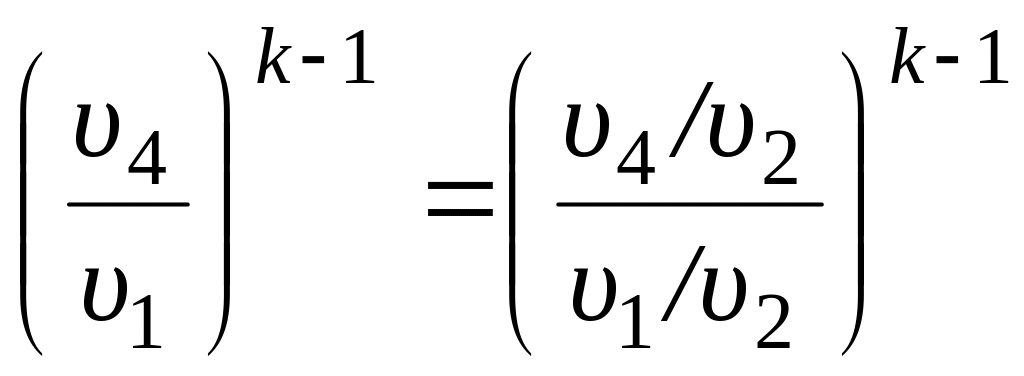. (30)

С учетом, что , и υ₂ = υ₃ (процесс 2 – 3 изохорный) получаем:

. (31)

Выражая из (29) температуру точки 5:

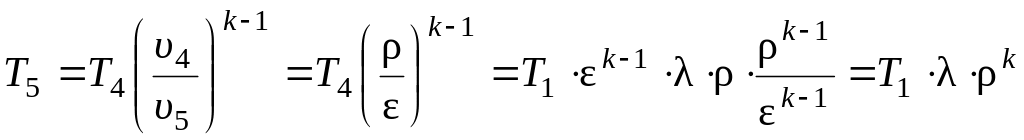. (32)

Подставив полученные значения температур всех характерных точек цикла в выражение (20), получим:

=

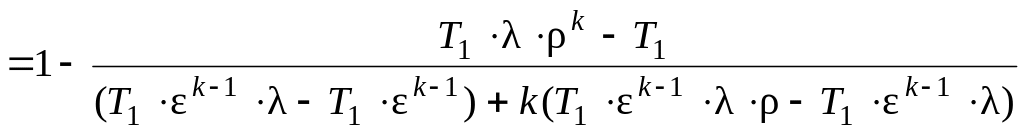. (33)

По формуле (33) произвести расчет термического КПД заданного цикла.

2.3.8. Термический КПД цикла Карно, который совершается в том же интервале температур определяется по формуле:

, (34)

где T_min и T_max – наименьшая и наибольшая температура среди рассчитанных температур цикла, К.

2.3.9. На основании выведенной формулы термического КПД цикла (33) построить графики зависимости η_t от характеристик цикла ε, λ, ρ, прил. 6.

Расчеты свести в табл. 7 – 9.

Т а б л и ц а 7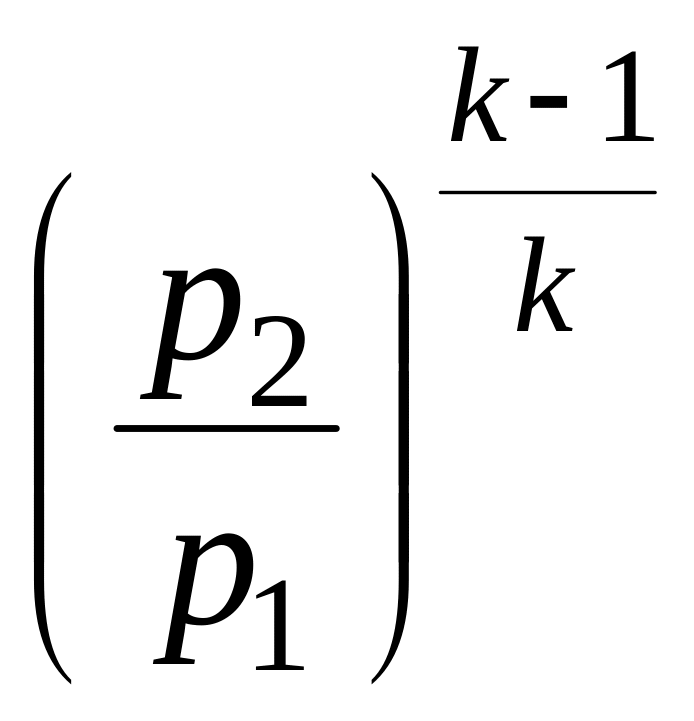
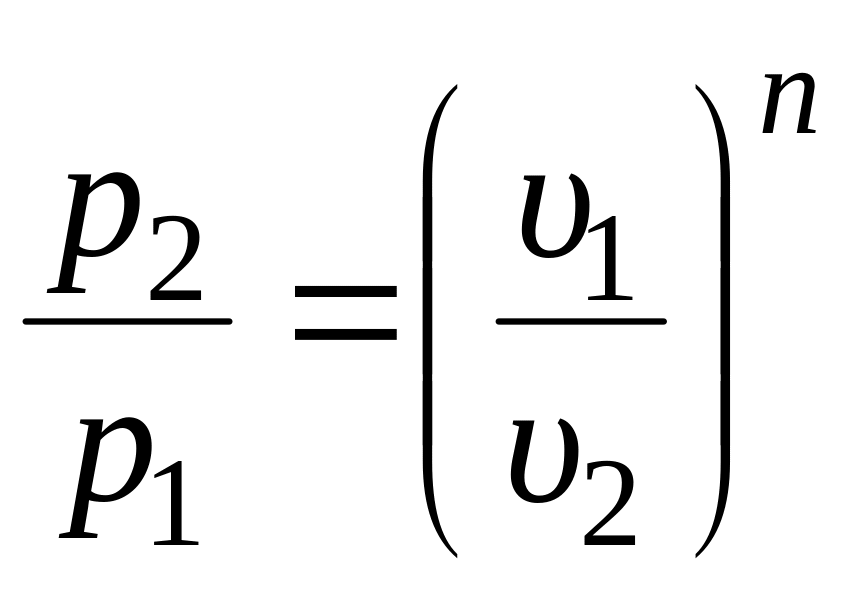