2.2. Расчет теплоемкостей газовой смеси

2.2.1. Средняя массовая изобарная теплоемкость смеси в интервале температур от 0 и t, ^оС, рассчитывается по формуле:

, кДж / (кг · К); (8)

где g_i – массовая доля i-го компонента заданной газовой смеси, по данным расчета; – средняя массовая изобарная теплоемкость i-го компонента в интервале температур от 0 до t, ^оС (определяется по прил. 3), кДж / (кг · К).

2.2.2. Средняя массовая изобарная теплоемкость смеси в интервале температур от t₁ до t₂, ^оС, рассчитывается по формуле:

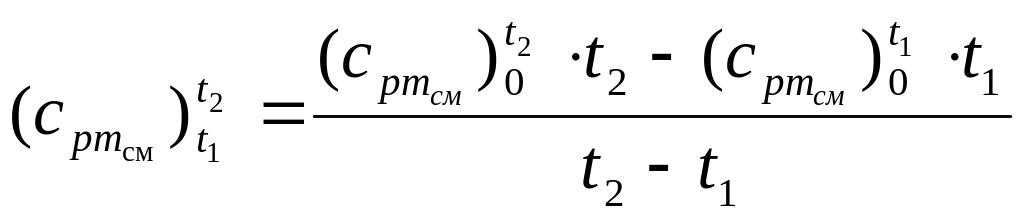, кДж / (кг · К).(9)

Входящие в (9) величины и рассчитываются по формуле (8).

2.2.3. Средняя массовая теплоемкость смеси при υ = const может быть рассчитан по формуле Майера, которая для рассматриваемого случая принимает вид:

, кДж / (кг · К). (10)

или

, кДж / (кг · К). (11)

2.2.4. По определению показателя адиабаты вычисляется его значение по соотношению:

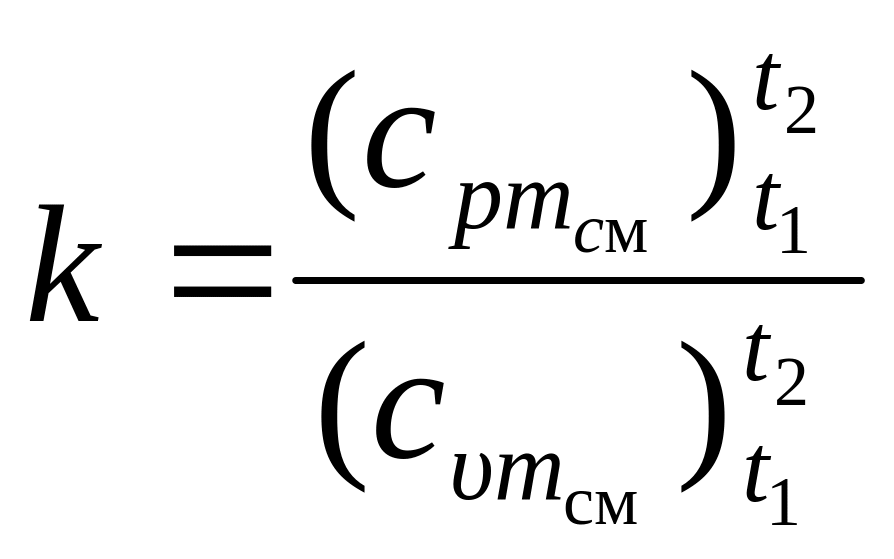. (12)

2.2.5. В соответствии с законами идеальных газов массовые, объемные и мольные теплоемкости связаны между собой определенными соотношениями:

кДж / (нм³ · К) (13)

или

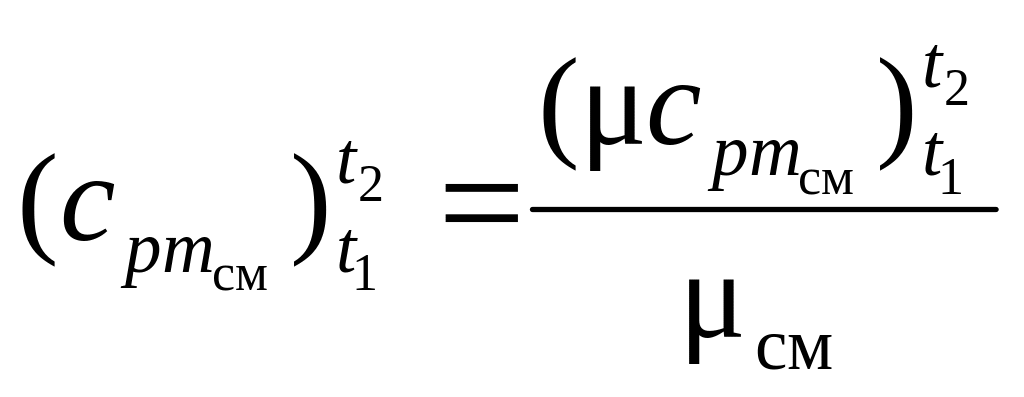, кДж / (кг · К), (14)

где μс – мольная теплоемкость, Дж / (моль ∙ К); μ – молярная масса вещества, кг / моль; 22,4 – объем 1 кмоля при нормальных условиях, нм³ / моль.

Из (13) и (14) при найденной средней молярной массе смеси μ_см и средней массовой теплоемкости смеси выражаются средняя объемная и мольная теплоемкости заданной газовой смеси.

Аналогично рассчитываются объемные и мольные теплоемкости смеси при υ = const по известным μ_см и .

2.2.6. Абсолютные значения теплоты рассчитываются по формулам:

, кДж (15)

, кДж (16)

, Дж (17)

где М, V, N – масса (кг), объем (нм³), число молей (моль) нагреваемой (охлаждаемой) газовой смеси соответственно, табл. 1; Q_M, Q_V, Q_N - теплоты, получаемые (отдаваемые) газовой смесью, имеющей массу М, объем V и число молей N.

2.3. Расчет термодинамического цикла

2.3.1. Расчет цикла начинается с нахождения параметров любой точки, для которой известны 2 параметра, третий – находится по уравнению Клапейрона для 1 кг газовой смеси:

p υ = R T, (18)

где р – давление, Па; υ – удельный объем, м³ / кг; R – газовая постоянная, Дж / (кг · К); Т – температура, К.

2.3.2. Затем рассчитываются недостающие параметры для остальных точек. Для этого используются соотношение между основными параметрами для каждого процесса (табл. 6), уравнение Клапейрона (18) и характеристики цикла ε, λ и ρ (табл.2).

Примечание: При расчете адиабатного процессе принимать показатель адиабаты k, вычисленный по (12).

2.3.3. Найденные значения р, υ, Т заносятся в табл. 3. На основании этих данных строится цикл в координатах р – υ (с соблюдением масштаба, прил. 6). В подрисуночной надписи приводятся названия каждого изображенного термодинамического процесса.

2.3.4. Подведенная (в процессах 2 – 3 и 3 – 4) или отведенная теплота (в процессе 5 – 1), работа изменения объема газовой смеси, изменения внутренней энергии и энтальпии, изменение энтропии в зависимости от вида процесса рассчитываются по формулам табл. 6.

2.3.5. Используя результаты расчетов, заполняется табл. 4.

2.3.6. Эффективность работы цикла определяется путем нахождения его термического КПД (η_t) по формуле

, (19)

где l_ц – работа цикла, Дж / кг; q₁ и q₂ – соответственно подведенная и отведенная теплота, Дж / кг.

2.3.7. Термический КПД, вычисленный по (19) зависит характеристик: степени сжатия ε, степени повышения давления λ и степени предварительного расширения ρ (табл. 2).

Рассмотрим, как выводится эта зависимость [1]. Будем считать, что теплоемкость рабочего тела с, кДж / (кг · К), имеет некоторое среднее значение и не изменяется во время цикла. Для нашего случая, эти теплоемкости можно обозначить = const и = const (это средние удельные теплоемкости смеси при р = const и υ = const соответственно).

Т аблица 6