9. Стандартні помилки та довірчі інтервали оцінок параметрів одно факторної моделі.
Для
b1=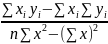
Довырчим ынтервалом випадкових величин b1 називають інтервал з межами (b1-∆b1); (b1+∆b1) в якому з певною наперд заданою ймовірністю Р=1-а знаходь істине значення параметра β. При цьому ймовір р=1-а назив довірчою ймовірністю.
Довжина інтервалу залежть від вибору рівня значимості а .
Стандартна помилка кутового коефіцієнта.
Стандартна помилка вільного члена:
=
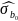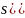
b0
=
b0±∆b0
∆b0=t
∆b0=t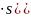
10. Кореляційний аналіз. Матриці r0, r1/
Коефіцєнт кореляції визначається за формулою:
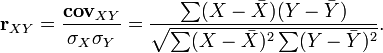
Значимість коеф. Кореляції перевіряється за Т-критерієм Стюдента:
Ті=
Якщо tрозр>tтабл., то коеф. Корел. Вважається істотним.
Якщо йдеться про багато факторну модель, то к-сть паних коеф. Корел. Збільш. Завдяки тому, що збільш кількість факторів моделі.
З них утворюється матриця кореляції нульового порядку R0. Це кореляційна матриця э симетричною відносно головної діагонаі
R0=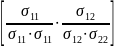
11. Скоригований коефіцієнт детермінації за Тейлом та Амемією
Коефіцієнт детермінації R2 показує, яка частина руху залежної змінної описується даним регресійним рівнянням, і обчислюється за формулою
R2=R2
–
(1- R2)
На значення коефіцієнта детермінації впливає кількість факторів, що враховано в моделі. Уведення в модель кожної нової змінної збільшує значення коефіцієнта детермінації. Тому щоб запобігти невиправданому розширенню моделі й мати змогу порівнювати моделі з різною кількістю факторів, уводять спеціальний оцінений коефіцієнт детермінації
де а2и - незміщена оцінка дисперсії залишків; а2у - незміщена оцінка дисперсії залежної змінної, а2 =------Y (уі - у)2.
п-1 і=1
Неважко помітити, що обидва коефіцієнти пов’язані такою залеж-ністю:
Обчислений у такий спосіб коефіцієнт детермінації називається скоригованим за Тейлом і позначається RT. Крім того застосовують також коригування за Амемією, яке виконується за формулою "
Обчислений у такий спосіб коефіцієнт детермінації називається скоригованим за Амемією і позначається RA.
12. Виявлення мульт. Та визгачення її рівня.
6. Алгоритм Феррара — Глобера складається із семи кроків.
6.1. Стандартизація (нормалізація) змінних
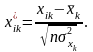
6.2. Знаходження кореляційної матриці
.
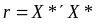6.3. Визначення критерію 2 (“хі”-квадрат)
6.4. Визначення оберненої матриці
.
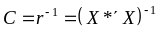6.5. Обчислення F-критеріїв
6.6. Знаходження частинних коефіцієнтів кореляції
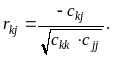
6.7. Обчислення t-критеріїв
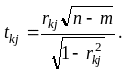
13. Природа та наслідки автокореляції збурення.
Вид моделі.
в якій вектор збурень не задовольняє класичним властивостям збурень:
1.
2.
Гомоскедастичність:
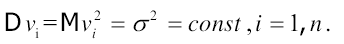
3.
Залежність збурень:
4.
Незалежність збурень та регресорів:
5.
Збурення
нормально розподілені для всіх i.
Наслідки автокорельованості збурень на оцінки методу найменших
квадратів:
1.Оцiнки МНК будуть незміщеними, але не будуть ефективними (не
матимуть найменшої дисперсії).
2.Стандартнi оцінки коварiацiйної матриці оцінки МНК будуть зміщеними,
i, як наслідок, процедури перевірки гіпотез та інтервального оцінювання,
основані на стандартних статистиках, будуть некоректними.
14. Тестування автокореляції збурення
Критерій визначення автокорельованості збурень Дарбіна-Уотсона.
Підраховується практичне значення статистики Дарбіна-Уотсона
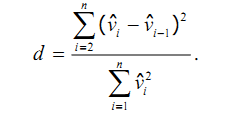
З таблиці Дарбіна-Уотсона знаходиться два числа dL та dU. В залежності від розташування точок на координатній прямій робиться висновок.
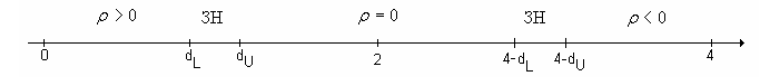
Робимо висновок за таким правилом:
Якщо d < dL, то має місце автокореляція з додатнім ρ.
Якщо dL < d < dU, то ми не можемо зробити ніякого висновку, і цей інтервал називається зоною невизначеності (ЗН).
Якщо dU < d< 4 – dU, то автокореляція відсутня.
Якщо 4 – dU < d < 4–dL, то ми не можемо зробити ніякого висновку. Цей інтервал також є зоною невизначеності (ЗН).
Якщо 4 – dL < d < 4, то має місце автокореляція з від’ємним ρ.