1. Параметричний критерій Гольдфельда-Квандта)

Цей тест також застосовується, коли помилки в економет- ричній моделі можна вважати нормально розподіленими випад­ковими величинами і відносно характеру гетероскедастичності є апріорні структурні обмеження. Припустимо, що дисперсії похи­бки прямо пропорційно залежать від величини деякої незалежної змінної, тоді тестування відбувається в такому порядку:

а) спостереження впорядковуються відповідно до величини Хі

б) з середини ряду вилучаються «с» значень;

в) окремо оцінюються два рівняння регресії для перших n1 =(n-с)/2 і останніх n2 =(n-с)/2 спостережень;

г) розраховується відношення Q = S22/ S12, де і - залиш­кові суми квадратів відповідно для менших та більших значень пояснюючої змінної.

Оскільки припускається відсутність кореляції між похибка­ми у вибірках, то суми квадратів, поділених на відповідне число ступенів свободи, являють собою дві незалежні величини, розпо­ділені як хі-квадрат. Ці дві величини є незміщеними оцінками ди­сперсії у вибірках

S12=e1’e1/n1-k

S22=e2’e2/n2-k

Q= S22/ S12

Дану величину, із зрозумілої причини, називають диспер­сійним відношенням. Величина Q при

F-розподіл з v1 i v2 ступенями свободи. Вона порівнюється з табличним значенням F-критерію для вибраного рівня значимос­ті а. Якщо Fрозр/Fтабл, приймається Н0.

2. Узагальнений метод найменших квадратів

Економетрична модель, якій притаманна гетероскедастичність, є узагальненою моделлю, і для оцінювання її параметрів слід скористатися узагальненим методом найменших квадратів. Розглянемо цей метод.

Нехай задано економетричну модель

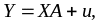
Задача полягає в знаходженні оцінок елементів вектора А в моделі. Для цього використовується матриця S, за допомогою якої коригується вихідна інформація. Ця ідея була покладена в основу методу Ейткена.

Базуючись на особливостях матриць Р і S, можна записати співвідношення між цими матрицями та оберненими до них.

Оскільки S — додатно визначена матриця, то вона може бути зображена як добуток 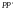, де матриця P є невиродженою, тобто: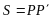

Коли ;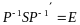

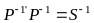
Помноживши рівняння ліворуч на матрицю 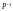, дістанемо:

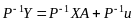
Позначимо ; ;

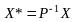Тоді модель матиме вигляд:

Оцінка параметрів , яку знайдено за допомогою (7.7), є оцінкою узагальненого методу найменших квадратів (методу Ейткена).

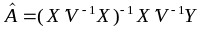, (7.12)

а для її коваріаційної матриці

.

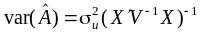3. Метод найменших квадратів в матричному вигляді.

Як і у випадку простої лінійної регресії, знаходять невідомі параметри за методом найменших квадратів, тобто мінімізують суму квадратів відхилень фактичних даних від теоретичних:

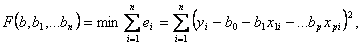
Звідки отримується нормальна система рівнянь

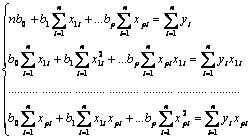
Розв’язуючи систему рівнянь (3) щодо b0, b1…bр одержують рівняння множинної регресії.

Лінійну багатофакторну модель, як і основні проблеми регресійного аналізу, зручно розглядати за допомогою матриць. Для цього введемо матриці:

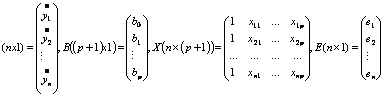
Тоді систему (2) можна записати у матричній формі

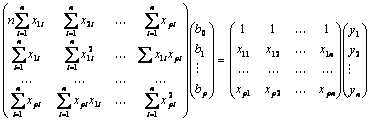
4. Властивості мнк оцінок:незаміщеність.

Оскільки згідно з першою умовою , то 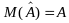. Отже, оцінка параметрів 1МНК є незміщеною.

Незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів 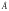. Якщо оцінка незміщена, то при багаторазовому повторенні випадкової вибірки попри те, що для окремих вибірок, можливо, були помилки оцінки, середнє значення цих помилок дорівнює нулю.

Різниця між математичним сподіванням оцінки і значенням оціненого параметра

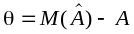(4.13)

називається зміщенням оцінки.

Не можна плутати помилку оцінки з її зміщенням. Помилка дорівнює і є випадковою величиною, а зміщення — величина стала.