Дробно-линейная функция.

 

Определение: Дробно-линейной функцией называется функция вида:

,

где a, b, c, d – const, c ≠ 0. Эта функция определена всюду, кроме  .

Выясним, как выглядит график этой функции. Приведем функцию к виду:

.

Обозначим   .

Тогда получим                                                                                        (1)

Согласно правилам преобразования графиков, график функции (1) может быть построен с помощью следующих действий:

1.                  построим график функции  ;

2.                      - сделаем параллельный перенос предыдущего графика вдоль оси ОХ на а₁ единиц влево или вправо;

3.                    - сделаем параллельный перенос предыдущего графика вдоль оси ОУ на b₁ единиц вверх или вниз.

Таким образом, графиком дробно-линейной функции является гипербола, центр которой находится в точке О₁ (а₁, b₁).

29. Предел функции в точке

Пусть функция f(x) определена в некоторой проколотой окрестности точки x₀ .

Число A называется пределом функции f(x) при x → x₀ (или в точке x₀), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x₀| < δ, справедливо неравенство |f(x) − A| < ε,   т.е. 

lim

x → x0

 f(x) = A           ε > 0    δ > 0 :     0 < |x − x₀| < δ  |f(x) − A| < ε.

Используем понятие окрестности и учтем, что

0 < |x − x₀| < δ  x  

·

O

 _δ (x₀ )   и     |f(x) − A| < ε  f(x)  O_ε (A).

(Точка над символом окрестности указывает, что это проколотая окрестность.)

Теперь определение предела функции в точке можно представить в виде

lim x → x0  f(x) = A           ε > 0    δ > 0 :     x   · O  δ (x0 )  f(x)  Oε (A).

Еше проще:

lim x → x0  f(x) = A           O (A)     · O  (x0) :     x   · O  (x0)  f(x)  O (A).

Геометрический смысл того, что x  

·

O

 (x₀)  f(x)  O (A) поясняет рис.1

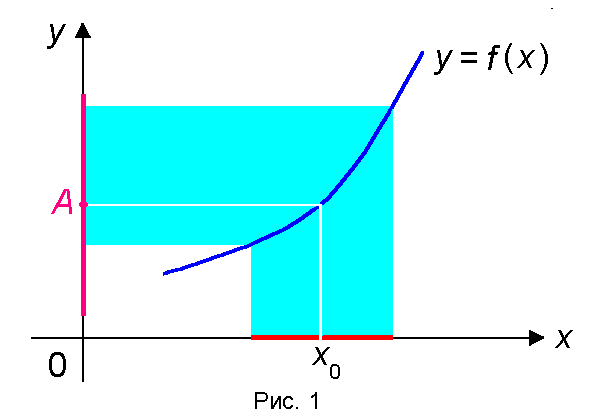
На этом рисунке проколотая окрестность 

·

O

 (x₀) точки x₀ изображена красным отрезком на оси OX из которого исключена точка x₀. Окрестность O (A) точки A изображена розовым отрезком на оси OY. Очевидно, что образ окрестности 

·

O

 (x₀) при отображении y = f(x) содержится в O (A).

30. Первый замечательный предел.

 

Рассмотрим функцию  . Эта функция при х=0 неопределенна. Рассмотрим   и докажем, что он равен 1. Заметим, что    и  . При вычислении   теорему о пределе дроби применять нельзя, так как предел знаменателя равен 0.

Рассмотрим окружность радиуса 1.  АОС – центральный угол, обозначим его через х, причем 0<х< .

 

Рассмотрим площади треугольников АОС и ВОС, и площадь сектора АОС. Из рисунка 19 видно

S_ΔАОС<S_{сектора АОС} <S_ΔВОС                                           (4)

S_ΔАОС=0,5·ОС·АD=0,5·sin x; S_{сектора АОС} =0,5·ОС2·АС=0,5·1·х=0,5х;

S_ΔВОС=0,5·ОС·ВС=0,5·1·tg x=0,5·tg x. Тогда неравенство (4) принимает вид:

0,5·sin x < 0,5·x < 0,5·tg x

Разделим обе части на 0,5·sin x, получим

<   < 

или

                   <   <  .                                              (5)

Неравенство (5) получено в предположении, что х>0. Оно верно и при х<0, так как при х<0 имеем   =   и cos (-x) = cos x.

Перейдем к пределу в двойном неравенстве (5) при х→0  .

Так как   и  , то по теореме 4 имеем, что

.                                                 (6)

Этот предел называется первым замечательным пределом.

График функции   имеет вид:

 

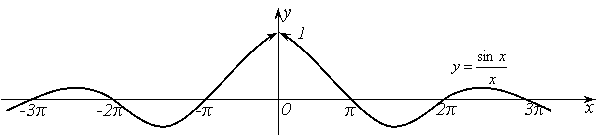
Рис. 20.

 

Примеры.

1.  .

2.      (k=const).

3.  .

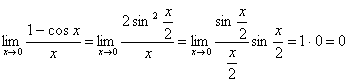4.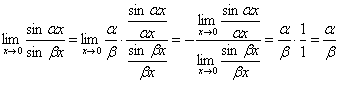   (α = const, β = const).