12. Функция .

1)                Область определения:  .

2)                Область значений – вся числовая прямая.

3)                 - основной период функции.

4)                Функция нечетная.

5)                Функция возрастает на промежутках  ,  .

График функции  изображен на рисунке 13.

 

 

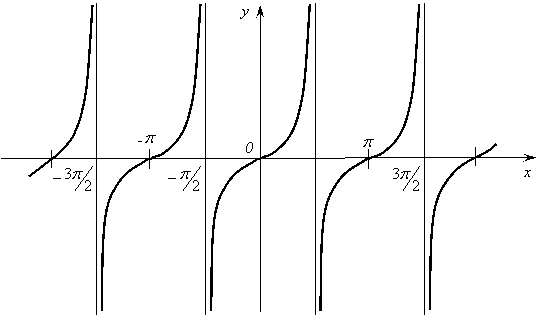
Рис. 13.

13. Функция .

1)                Область определения:  .

2)                Область значений – вся числовая прямая.

3)                Функция периодическая с основным периодом  .

4)                Функция  нечетная.

5)                Функция   убывает на промежутках  ,  .

График функции  изображен на рисунке 14.

14. Функция  является обратной к функции  .

1)                Область определения – отрезок  .

2)                Область значений – отрезок  .

3)                Функция нечетная:  .

4)                Функция возрастающая.

Из сказанного выше следует, что записи   и  ,  , эквивалентны. Подставив в равенство   вместо   его выражение, то есть  , получим  . Следовательно, для любого   из   имеем:

,   .

Последние два соотношения позволяют истолковать , где  , так:  - это число, взятое в пределах от   до   и такое, что его синус равен .

График функции   изображен на рисунке 15.

 

 

Рис. 15.

15. Функция  является обратной к функции  .

1)                Область определения – отрезок  .

2)                Область значений – отрезок  .

3)                Функция не является ни четной, ни нечетной.

4)                Функция убывающая.

Из сказанного выше следует, что записи   и  ,  , эквивалентны. Подставив в равенство   вместо   выражение  , получим  . Следовательно, для любого   из   имеем:

,   .

Последние два соотношения позволяют истолковать  , где  , так:   - это число, взятое в пределах от   до   и такое, что его косинус равен  .

Отметим, что имеет место следующее тождество:

.

В его справедливости можно убедиться с помощью графика функции  , изображенного на рисунке 16.

 

Рис. 16.

 

16. Функция   является обратной к функции  .

1)           Область определения – множество всех действительных чисел.

2)           Область значений функции – интервал  .

3)           Функция нечетная:  .

4)           Функция возрастающая.

Из сказанного выше следует, что записи   и  ,      , эквивалентны. Для любого   имеем:

,       .

Последние соотношения позволяют истолковать   так:   - это число, взятое в пределах от   до   (исключая сами значения   и  ) и такое, что его тангенс равен  .

График функции   изображен на рисунке  17.

 

Рис. 17.

 

17. Функция   является обратной к функции  .

1)                Область определения – множество всех действительных чисел.

2)                Область значений функции – интервал  .

3)                Функция не является ни четной, ни нечетной.

4)                Функция убывающая.

Из сказанного выше следует, что записи   и  ,      , эквивалентны. Для любого   имеем:

,       .

Последние соотношения позволяют истолковать   так:   - это число, взятое в пределах от   до  (исключая сами значения   и ) и такое, что его котангенс равен  .

Имеет место тождество

.

График функции   изображен на рисунке 18.

 

Рис. 18.