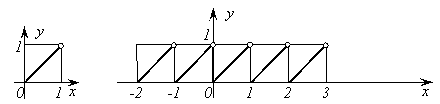|
Первый замечательный предел: |
|
Второй замечательный предел: |
|
Другие полезные формулы пределов: |
|
28. Основные элементарные функции.
Рассмотрим свойства и графики основных простейших функций.
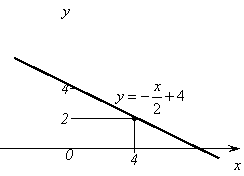
1. Линейная
функция. Линейной
функцией называется
такая функция, которая задаётся
формулой 
,
где k и b–
действительные числа. Если, в частности, k=0,
то получаем постоянную функцию 
;
если b=0,
то получаем прямую пропорциональность 
.
Свойства линейной функции при k≠0, b≠0:
1) Область определения функции – множество всех действительных чисел.
2) Функция ни четна, ни нечетна.
3) При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой.
Теорема. Графиком линейной функции является прямая.
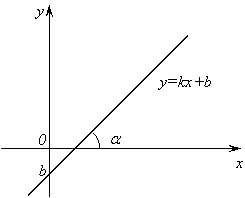
Рис. 1.
Число k называется угловым
коэффициентом прямой,
оно равно тангенсу угла 
между
прямой и положительным лучом оси х,
то есть 
.
2. Обратная
пропорциональность. Обратной
пропорциональностью называют
функцию, заданную формулой 
,
где k≠0.
Число k называют
коэффициентом обратной пропорциональности.
1) Область определения – множество всех действительных чисел, кроме нуля.
2)
-
нечётная функция (поскольку 
.
3) Если k>0, то функция убывает на промежутке (0;+∞) и на промежутке (-∞;0). Если k<0, то функция возрастает на промежутке (-∞;0) и на промежутке (0;+∞).
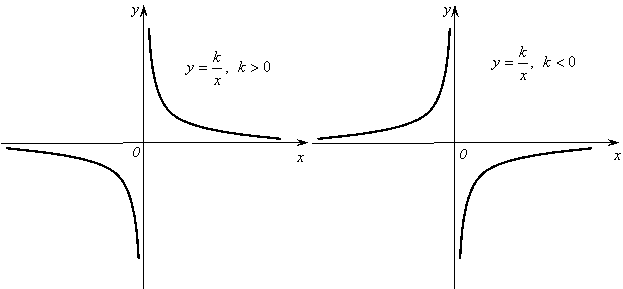
Рис. 2.
График обратной пропорциональности называют гиперболой.
3. Функция 
.
1) Область определения – вся числовая прямая.
2)
-
чётная функция 
.
3) На промежутке [0;+∞) функция возрастает.
4) На промежутке (-∞;0] функция убывает.
Графиком функции является парабола. Этот график изображен на рисунке 3.
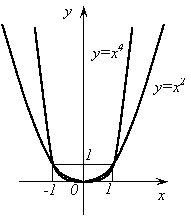
Рис. 3.
4. Функция .
1) Область определения функции – вся числовая прямая.
2)
-
нечётная функция 
.
3) Функция возрастает на всей числовой прямой.
График функции изображен на рисунке 4. Он называется кубической параболой.
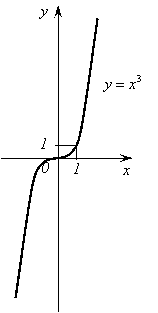
Рис. 4.
5. Функция .
1) Область
определения – луч [0;+∞).
Это следует из того, что выражение 
определено
лишь при х≥0.
2) Область значений - [0;+∞).
3) Функция ни четна, ни нечётна.
4) Функция возрастает на луче [0;+∞).
График функции изображен на рисунке 5.
Рис. 5.
6.
Функция 
-
целая часть числа. Если 
1,
то 
;
если 
2,
то 
;
если 
0,
то 
и
т.д. График функции
изображен
на рисунке 6.
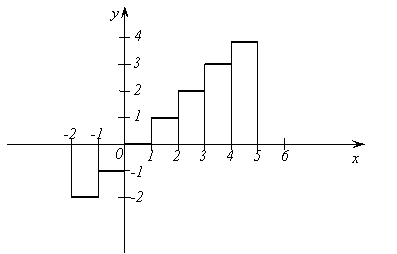
Рис. 6.
7.
Функция 
- дробная
часть числа. Построим график функции
.
Заметим, что 
,
поэтому достаточно сначала построить
ветвь графика на любом промежутке
длиной 1,
например на 
.
Если
1,
то 
,
а потому
.
На рисунке 7 изображен график функции на промежутке , а на рисунке 8 изображен график функции на всей числовой оси.
|
|
|
|
Рис. 7. Рис. 8.
8.
Показательная функция. Показательная
функция задается
формулой 
,
где 
0 и 
.
1) Область определения функции – вся числовая прямая.
2) Область
значений функции – промежуток 
.
3) Функция
не является ни четной, ни нечетной. Это
следует из того, что 
и 
.
4) Функция возрастает на всей числовой прямой.
График показательной функции изображен на рисунке 9.
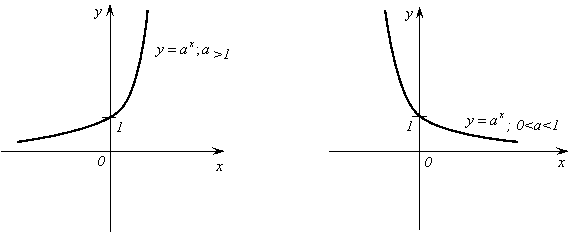
Рис. 9.
9.
Логарифмическая функция. Логарифмическая
функция 
является
обратной к показательной функции
и
обладает следующими свойствами:
1) Область определения – .
2) Область
значений – 
.
3) Функция ни четная, ни нечетная.
4) Функция
возрастает на промежутке
при
1,
убывает на
при 
1.
График функции изображен на рисунке 10.
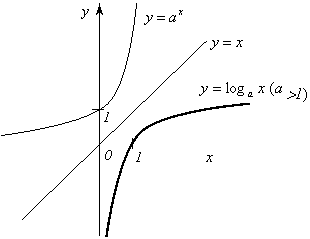
Рис. 10.
10.
Функция 
.
1) Область определения – множество всех действительных чисел.
2) Область
значений – отрезок 
.
3) Функция
периодическая; основной период равен 
.
4) Функция нечетная.
Функция
возрастает на промежутках 
и
убывает на промежутках 
, 
.
График функции изображен на рисунке 11.
|
|
|
|
Рис. 11.