Вопрос 26. Описание и анализ потоков информации с использ. Графов.

Модели описания и анализа потоков информации на основе графов.

Основным носителем информации в информации в организационных системах являются документы. Документы как для системы в целом, так и в рамках отдельных подсистем можно разделить на входные, выходные и промежуточные. Между документами основными отношениями часто являются отношения вхождения и порядка. Отношения вхождения означает, что некоторый документ X_{j} формируется на основе докуметов:  . Отношение порядка   означает, что документ   может быть сформирован только тогда, когда закончится формирование  . Потоки информации в информационных системах образуются также движением реквизитов, показателей, различных сообщений данных. Поэтому говоря об элементах потоков информации будем иметь ввиду все вышеперечисленное. Элементам потока информации можно поставить в соответствие вершины графов   -- соединяются дугой от   к , если   является входом для  (т.е. включается в него или обязательно для его формирования). Полученный граф называют информационным графом. Матрицу смежности его будем обозначать  . Наличие такой матрицы смежности позволяет использовать строгие процедуры обработки. Будем последовательно находить степень матрицы смежности. Будем формировать матрицу смежности   до тех пор, пока не окажется, что  , а   -- такая ситуация возможна, если информационный граф не имеет замкнутых контуров (циклов с учетом направления). В противном случае нулевая матрица не будет получена никогда и показателем того, что есть контуры, будет неравенство нулевой матрицы матрице  , где  -- число вершин. ... определяется матрицей достижимости:  -- такая матрица будет для всех пар, прямо или косвенно зависящих друг от друга элементов.

На основе матрицы достижимости и матриц  , где   анализируют формальные свойства графов.

• Порядок элемента \pi _{j} -- длина наибольшего элемента, связывающего  -ый элемент с некоторым -ым элементом. Формально он определяется следующим образом:

где 

Физ. смысл порядка: номер такта, к которому готовы все составляющие элемента 

• Порядок информационного графа

Если для числа   справедливо соотношение:  ,   (т.е. нет контуров) -- такая схема называется  -тактной.

• Признак контура -- им является появление ненулевых элементов на главной диагонали любой из матриц A^{k}.

Наличие контура свидетельствует либо об ошибке в обследовании, либо о неправильно спроектированном документообороте. В любом случае, необходим содержательный анализ с целью устранения контура.

• Равенство нулю суммы элементов

  -го столбца матрицы смежности говорит о том, что элемент   является входным.Равенство нулю говорит о том,что элемент   является выходным (т.е. от него ничего не зависит)

• Если для некоторого элемента   сумма соответствующей строки и соответствующего столбца матрицы смежности равны нулю, то этот элемент к рассматриваемой схеме вообще не имеет отношения.

Тогда этот элемент одновременно выходной и входной Длина пути 8. Число всевозможных путей 9. По аналогии со свойством 4 и 5 отличные от нуля элементы  -го столбца матрицы достижимости   указывает все элементы информационного потока, которые учавствуют в формировании элемента   Отличные от нуля элементы  -той строки этой же матрицы указывают все элементы при формировании которых используется элемент   10. Максимальное значение порядка элемента  -ой строки матрицы смежности  , которые неравны нулю, определяет номер такта  , после которого элемент  уже не используется и может быть стерт с памяти системы.  ;   11. число тактов, в течении которых элемент   должен храниться в памяти системы, определяется соотношением:  -- порядок определяет, когда элемент может быть сформирован и готов.  -- время, когда он уже не использования 12. анализ структуры всех путей, связывающих элементы   и   позволяет выявить как дублирующие связи, так и дублирующие элементы, что позволяет улучшить свойства анализируемого информ потока(самый простой способ анализа: запустить волновой алгоритм)

Пример:

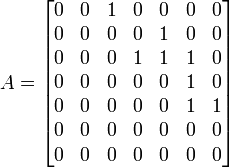- - запишем матрицу смежности: по ней можем сказать, что элементы 1 и 2 -- входные, элементы 7 и 6 -- выходные

Возведем матрицу в квадрат:

Ч исло "2" говорит о том, что элемент 6 может быть получен из элемента 3 двумя разными путями длины 2 (т.к. квадрат матрицы): путь 3-4-6 и путь 3-5-6.

Возводим матрицу в куб:

Матрица в четвертой степени уже равна нулевой матрице. Таким образом,  ,   -- схема трехтактная.

Теперь находим сумму матриц: 

В идим, что из вершины 1 -> 6, равно как и из 3 -> 6 есть три равных пути длиной от 1 до 3.

Определим порядок элемента номер 5, например: порядок 2, т.к при  столбец 5 нулевой -- значит, все составляющие элемента 5 получаются готовыми ко второму такту (сам элемент на 2-ом такте будет получен). Сколько нам его хранить в памяти: смотрим 5-ую строчку в матрице смежности: в ней 2 ненулевых элемента: 6 и 7. Найдем порядок элементов 6 и 7:   (нашли ранее),  ,  . Следовательно: ( ),   -- храним мы 5-ый элемент всего 1 такт.