Семинар №5 Рост эпитаксиальных слоев из газовой фазы.
Получение эпитаксиальных слоев кремния хифидным методом
Соотношение исходных компонентов
H2 : SiCl4 = 150:1
Температура процесса
T = 1223 K
Проточная система.
Найти:
равновесный состав газовой фазы для заданной T и соотв. соотношения для исходных компонентов.
Выход кремния β(%)
Скорость роста э.с. f
Введем обозначения для равновесных мольных концентраций компонентов:
m1 = CSiHCl3
m2 = CHCl
m3 = CSiCl4
m4 = CSiCl2
m5 = CH2
m6 = CSi
Решение:
Механизм взаимодействия SiCl4 c H2 в общем виде :
SiCl4 + 2H2 = Siтв + 4 HCl (I)
Реально представить в несколько стадий:
SiCl4 + H2 = SiHCl3 + HCl (1)
SiHCl3 = SiCl2 + HCl (2)
SiCl2 = 0,5Si + 0,5 SiCl4 (3)
SiCl2 + H2 = Si + 2HCl (4)
Термодинамический анализ процесса:
константы равновесий для реакций 1-4, включающие равновесные парциальные давления компонентов паро-газовой фазы и активности компонентов конденсированной фазы ( αSi может быть приравнена к 1) :
для реакции (1) Δ∂ = (1+1) – (1+1) = 0
Чтобы выразить Kp через мольные концентрации Ci
ур. Клайперона-Менделеева
Pi V = ni RT
Pi = RTn/V = Ci RT, νi – стехиометрический коэффициент.
;
в момент равновесия в газовой фазе Σm
= m1+m2+m3+m4+m5
Для реакции (2) Δ∂ = (1+1) – (1) = 1
(6)
Для реакции (3) Δ∂ = (0,5) – (1) = -0,5
(7)
Для реакции (4) Δ∂ = 2 – (1+1) = 0
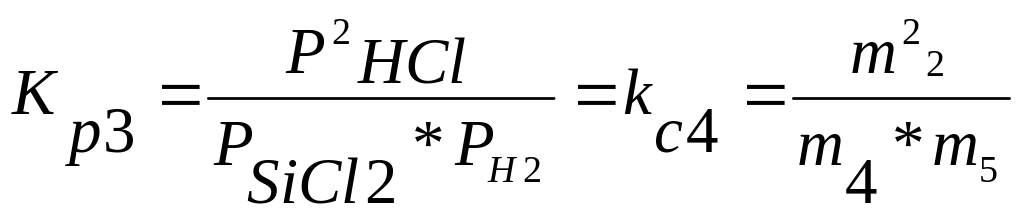(8)
Кp1 *Кp2 *К2p3 = Кp4 , имеем только 3 уравнения для определения констант равновесия независимых реакций ( при шести неизвестных m1-m6 ).
Составим еще 3 уравнения материального баланса:
по Si
(9)
Вводится один моль SiCl4 который даст 1 моль Si и 2 моля Cl2
по H2
(10)
по Cl2
(11)
Систему из 6 уравнений (6-8) и (9-11) с шестью неизвестными можно свести к системе из двух уравнений с 2-мя неизвестными.
Выразим m4 из (8), а m1 из (6)
через m2 m5
;
m3
из
(7)
Подставим m1, m3, m4 в уравнение (10) и (11)
В
ур. (10)
(12)
В
ур. (11)
(13)
Анализ уравнения I позволяет достаточно точно оценить значение Σm и пределы изменения m2 и m5
SiCl4 + 2H2 = Siтв + 4 HCl
Введено: 1 моль 150 моль
До начала реакции
Σmнач = 150 + 1 = 151 моль.
151 < Σm < 152
Оценочно Σm = 151,5
После окончания реакции
Σmкон = (150 – 2)моль H2 + 4 моль HCl = 152 моль.
0 < m2 < 4
148 < m5 < 150
Зависимость Kp от температуры:
,
интегрируем ( пусть ΔH
≠ f(T)
)
ΔG=ΔG0 + RT ln Kp , в равновесии ΔG=0.
ΔG0 = -RT ln Kp
ΔG0 = ΔH0 – TΔS
ln Kp = -ΔH0 / RT + ΔS0 / R.
Для
уравнение
Клазиуса – Клайперона.
Энтальпия реакции ΔH0 не зависит от Т если примем, что теплоемкость Cp = 0 в интервале температур.
;
ΔH0
=
ΔH0 298
;ΔS0
=
ΔS0 298
Необходимо найти ΔH0 и ΔS0 для реакций (2)-(4)
ΔHf и ΔSf - энтальпия и энтропия образ. 1 моля в-ва из простых в-в при 298 К.
γi и γj – стехиометрические коэф. в реакции.
|
SiCl4 (г) |
H2 (г) |
Si (тв) |
HCl (г) |
SiHCl3 (г) |
SiCl2 (г) |
ΔHf 298 кДж/моль |
-657,01 |
0 |
0 |
-92,312 |
-512,96 |
-165,64 |
ΔSf 298 кДж/моль |
330,62 |
130,57 |
18,83 |
186,79 |
313,76 |
281,83 |
Для реакции (2)
Для реакции (3)
Для реакции (4)
;
Уравнения 12 и 13 можно переписать
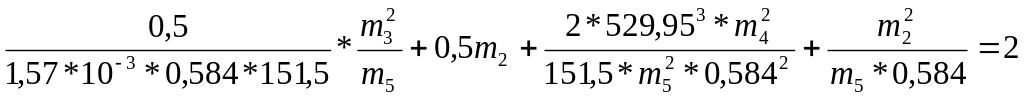
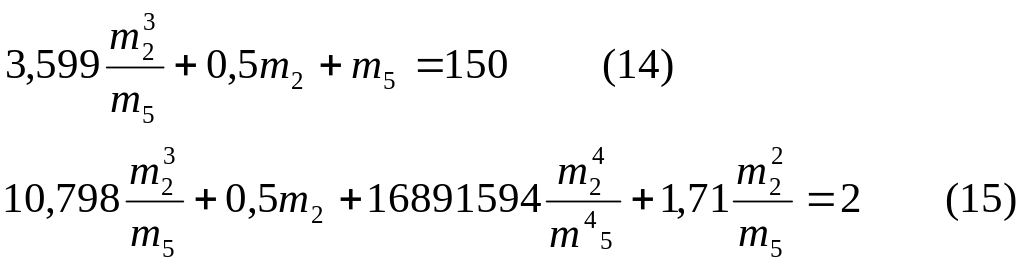
m5 |
m2 |
Правая часть уравнения (14) |
Правая часть уравнения (15) |
149 |
1,744 |
150,00012 |
1,604 |
148,87 |
1,919 |
150,0003 |
1,9807 |
148,86 |
1,932 |
150,0003 |
2,0113 |
148,865 |
1,925 |
149,99995 |
1,99478 |
148,864 |
1,926 |
149,99972 |
1,99714 |
148,863 |
1,928 |
150,00026 |
2,00182 |
m5
= 148,863
m2 = 1,928
Из уравнения (9) найдем m6
m6 = 1- m1 - m4 - m3 = 1 – 0,3466 – 0,0427 – 4,48*10-4 = 0,6103 .
Равновесный выход конденсирующего элемента (Si)
(61,03%)