16, Выполнение операций двоичной арифметики.

Арифметические операции в двоичной системе счисления

       Из всех позиционных систем особенно проста двоичная система счисления. Рассмотрим выполнение основных арифметических действий над двоичными числами. 

     Все позиционные системы счисления "одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

• справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;

• справедливы правила сложения, вычитания и умножения столбиком;

• правила выполнения арифметических операций опираются на таблицы сложения и умножения.

Сложение

 

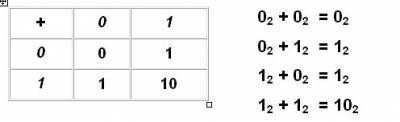
Рассмотрим примеры на сложение. 

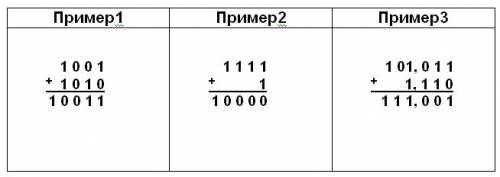
     При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица.

     Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.

Вычитание

 

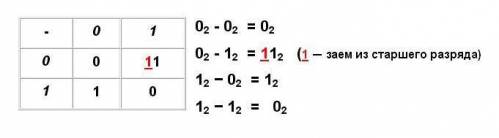
     Рассмотрим примеры  на вычитание. 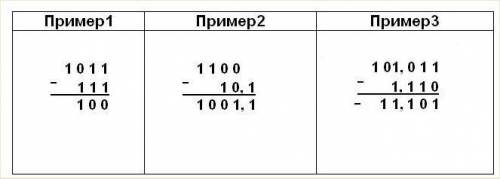       При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак. Умножение       Рассмотрим примеры  на умножение.      Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя. Рассмотрим примеры  на умножение.      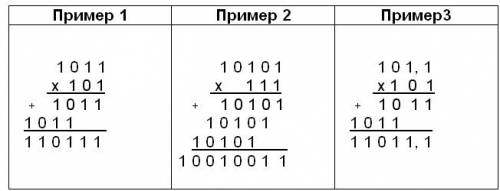При выполнении умножения в примере 2 складываются три единицы 1+1+1=11 в соответствующем разряде пишется 1, а другая единица переносится в старший разряд. В двоичной системе счисления операция умножения сводится к сдвигам множимого и сложению промежуточных результатов. Деление      Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.      Рассмотрим примеры на деление

17, Формы и форматы, используемые для представления чисел в эвм.

Формы представления чисел в ЭВМ

Машинным изображением числа называют его представление в разрядной сетке ЭВМ. В вычислительных машинах применяются две формы представления чисел:

• естественная форма или форма с фиксированной запятой (точкой);

• нормальная форма или форма с плавающей запятой (точкой);

Пример:

(естественная форма) 452,34 = 452340*10^-3 = 0,0045234*10⁵ = 0,45234*10³(нормальная форма)

Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме:

X₁₀ → X₂ = M₁ × [10₂]^r

После этого осуществляется ещё одна важная процедура:

• мантисса с её знаком заменяется кодом мантиссы с её знаком;

• порядок числа с его знаком заменяется кодом порядка с его знаком.

Указанные коды двоичных чисел - это образы чисел, которые и воспринимают вычислительные устройства. Каждому двоичному числу можно поставить в соответствие несколько видов кодов.

Существуют следующие коды двоичных чисел:

• Прямой код;

• Обратный код;

• Дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Содержание  [убрать] 1 Естественная форма 2 Нормальная форма 3 Прямой код 4 Обратный код 5 Дополнительный код 6 Литература

Естественная форма

В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.

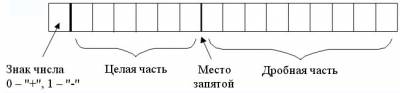
Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.

A = [A] · K^А,

где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, K^А - масштабный коэффициент.

Естественная форма числа в неявном, условном виде реализуется формулой:

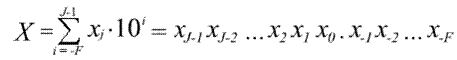
т.е. число записывается только с помощью набора значащих цифр x_j без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

Нормальная форма

С плавающей запятой (ПЛЗ) числа изображаются в виде:

X = ± M×P ^±r,

где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×10², 0,36×10^-2, –0,1082×10³.

Нормализованная экспоненциальная запись числа - это запись вида a= m*P^q, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом m - мантиссa числа, q - порядк числа.

Tо есть нормальная форма реализуется формулой: 

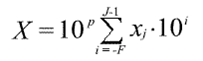
Нормальная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

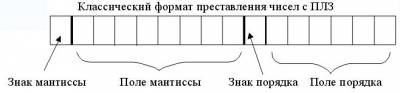
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, используется так называемый смещённый порядок, который рассчитывается по формуле 2^(a-1) + ИП, где a - количество разрядов, отводимых под порядок, ИП - истинный порядок.

В конкретной ЭВМ диапазон представления чисел с плавающей запятой зависит от основания системы и числа разрядов для представления порядка. При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Точность вычислений при использовании формата с плавающей запятой определяется числом разрядов мантиссы. Она увеличивается с увеличением числа разрядов.

Алгоритм представления числа с плавающей запятой:

1. перевести число из p-ичной системы счисления в двоичную;

2. представить двоичное число в нормализованной экспоненциальной форме;

3. рассчитать смещённый порядок числа;

4. разместить знак, порядок и мантиссу в соответствующие разряды сетки.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена информацией, экономии памяти и удобства операций над десятичными числами предусматриваются специальные форматы их представления: зонный (распакованный) и упакованный. Зонный формат используется в операциях ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.