90. Новые типы ф-нтов: ф-нты в вытрамбованных котлованах, щелевые ф-нты, ф-нты с наклонной подошвой и др.
Надеюсь, он вам не попадется... ;)
91. Основные предпосылки расчета и предварительный подбор сечения ф-нта.
К
гибким ф-нтам относят ф-нты с соотношением
,
d-высота
конструкции ф-нта, L-длина.
К ним относят ленточные и плитные ф-нты.
Гибкость ф-нтов, в соответствии с работами
Симвулиди, Горбунова-Посадова, Жемочкина,
оцениваются спец выражениями-функциями
жесткости ф-нтной балки, ее длины и
модулей деформируемости основания. В
зависимости от величины этой ф-ции при
заданной нагрузке опред Mx
и Qx.
При расчете применяются две теории:
- теория местных упругих деформаций;
-теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
92.Теория местных упругих деформаций, пределы применимости.
Предпосылкой
является положение о прямой
пропорциональности между давлением и
местной осадкой или осадкой только в
месте приложения нагрузки. Основное
уравнение деформ в теории является
,
где y-упругая
осадка в месте приложения напряж.;
-давление
по подошве ф-нта;
-коэф
упругости основания.
М
етод
учитывает деформ только в пределах
поверхности загружения, вне пределах
деформ не учитываются. Применим для
слабых грунтов.
93. Теория общих упругих деформаций, пределы применимости.
Метод базируется на на решениях теории упругости для однородных изотропных тел, кот в опред пределах примен и для грунтовых оснований. Исходные уравн:
-для
случая плоской задачи ф-ла Фламана
.
-
для
случая пространственной задачи ф-ла
Бусинеско
,
y-осадка
упругого полупространства;P-сосредоточенная
сила;
коэф деформируемости полупространства;D-
постоянная интегрирования.
Деформамации рассматриваются как в пределах нагруженной площадки, так и заее.
94. Предварительных подбор сечения фундаментных балок.
Д
ля
расчетов используют диф ур прогибов
изогнутой оси балки
.
Для назначения предварит размеров балка
рассматривается как жесткая и размеры
балки опред по известным ф-лам смеха
или сопромата.
;
;
.
Определив P1, P2, прикладываем их к балке. Для любого сечения балки определяем величины Mx и Qx и строим эпюры. По Mmax и Qmax определяем размеры и форму поперечного сечения. Зная размеры балки, полученные из W, вычисляем ее жесткость EJ.
95. Расчет фундаментных балок на местном упругом основании.
Исходными
усл расчета являются уравн изогнутой
оси балки
Дифференцируя дважды
;
;
;
Решением данного диф ур-я является выражение
.
-линейная
хар-ка балки на упругом основании.
.
96. Расчет фундаментных балок и плит на линейно деформируемом полупространстве.
1)Метод Горбунова-Посадова. Заключается в совместном решении ду изгиба балок и уравн деформации грунтового основания как линейно-деформир полупространства.
.
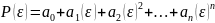2) Метод Симвулиди. Автором изходя из ду изогнутой оси балки и уравн деформ грунтов для опред реакций основания предлагается:
.
Х-координаты длины балки. Для опред
неизвестных ai
кроме двух усл равновесия и двух граничных
усл пользуются 4мя усл контактности
балки с основанием: 1)равенство прогиба
балки и осадка грунта на левом конце
балки. 2) равенство прогиба балки и осадка
грунта в середине балки. 3)равенство
площадей, образованных прогибами обеих
линий деформ. 4)равенство 3их производных
обеих функций в середине балки.
3) Метод Жемочкина. Основан на применении к расчету общей теории смеха СНС. Дает возможность получить решение с достаточной для практических целей точностью для любого вида балок. В основу положены допущения: 1)распред реактивных давлений по подошве ф-нтной балки принимается ступенчатым; 2)в пределах каждой ступени реакция грунта усредняется, принимается равномерной по длине ступени заменяется жестким шарнирным стержнем, приложенным к середине каждой ступени. Полученная система рассматр как фунд. балка, леж на сплошном лин.-деформ основании.
Для нахождения неизвестных составляем сист уравн равновесия. Опред перемещения прогиба балки. Строится эпюра реактивных давлений с величиной интенсивности на каждом участке ступени. Зная реактивные давления основания и внешние силы, действ на балку, определяем величины Qx и Mx в любом сечении балки.