6. Гистограмма

- это диаграмма столбцов, показывающая число точек, по­па­дающих в заданный интервал (класс, карман). Это число точек обычно называют частотой.

Кроме абсолютной частоты, при построении гис­тограмм иногда ис­поль­зуется относительная частота или частость. Ее по­лучают путем деления аб­солютной частоты на общее число обсле­до­ван­ных деталей (на­блюдений).

Три важных параметра гистограммы:

• центр;

• ширина;

• фор­ма.

Таблица 6.1.

Таблица частот

для распределения деталей по твердости HB покрытия

Номер ин­тервала	Интервал Изменения HB	Середина интервала	Частота	Частость
1	350 < HB  360	355	0	0,00
2	360 < HB  370	365	1	0,01
3	370 < HB  380	375	5	0,05
4	380 < HB  390	385	13	0,13
5	390 < HB  400	395	24	0,24
6	400 < HB  410	405	23	0,23
7	410 < HB  420	415	16	0,16
8	420 < HB  430	425	12	0,12
9	430 < HB  440	435	4	0,04
10	440 < HB  450	445	2	0,02
Итого:			100	1,00

Абсолютная частота, ед.

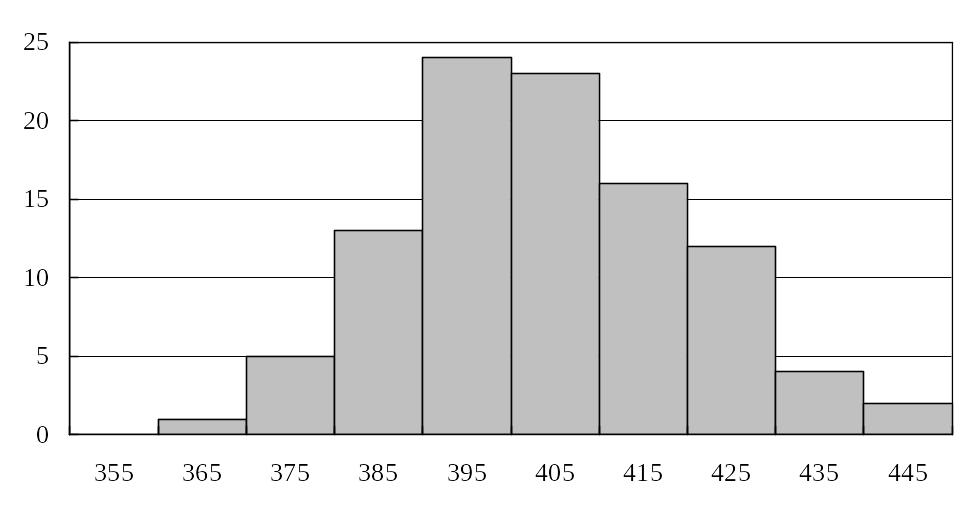
Твердость покрытия HB, кГ/мм²

Рис. 6.1. Гистограмма распределения деталей по твердости покрытия

Типичные формы гистограмм

а). Обычная (колоколообразная) гистограмма (рис. 6.2, а);

б). Гистограмма распределения с дву­мя пиками (рис. 6.2, б);

в). Гистограмма типа плато (рис. 6.2, в);

г). Гистограмма гребенчатого (мультимодального) типа (рис. 6.2, г);

д). Гистограмма положительно ско­шен­ного распределения (рис. 6.2, д);

е). Гистограмма усеченного слева распределения с поло­жи­тель­но ско­шенным "хвостом" (рис. 6.2, е);

ж). Гистограмма с изолированным пиком (рис. 6.2, ж);

з). Гистограмма с пиком на краю (рис. 6.2, з).

­

а) б)

в) г)

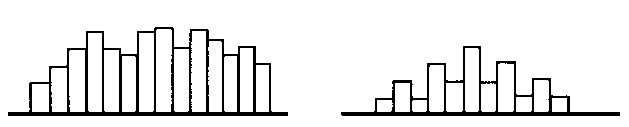
д) е)

ж) з)

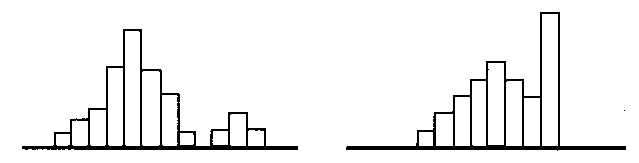
Рис. 6.2. Типичные структуры гистограмм

Индексы воспроизводимости

показывают воз­мож­ности процессов выполнять требования к качеству продукции.

Индекс воспроизводимости C_P определяется как отношение ширины по­­ля допуска параметра к фактическому разбросу параметра про­цесса. Если заданы двухсторонние границы допуска,

(6.1)

где S_U, S_L - верхняя и нижняя граница допуска соответственно;

 - среднее квад­ратическое отклонение (с.к.о.) параметра процесса.

Если заданы односторонние границы допуска, то индекс вос­про­из­во­ди­мос­ти определяется относительно среднего значения _X:

. (6.2)

В случае, если возможно смещение среднего значения _X гистограммы от­­носительно середины поля допуска, используют индекс C_PK воспроизводимости процесса, который определяется как ми­ни­маль­ное значение из двух:

. (6.3)

Таблица 6.2.

_{Доля брака (1- P) в зависимости от значения Ср}

Cp	0,7	0,9	1,0	1,1	1,2	1,3	1,33	1,4	1,5	1,67	2,00
1-P	3,6%	0,69%	0,27%	0,097%	318 ppm	96 ppm	63 ppm	27 ppm	6,8 ppm	570 ppb	2,00 ppb
Сокращение ppm обозначает число частей (изделий) на миллион, ppb - на миллиард. Таким образом, 1ppm = 0,0001%; 1ppb = 0,0000001%.

Таблица 6.3.

Нормы для индекса воспроизводимости C_P 

Характеристика процесса	CP
Существующие процессы	1,33
Новые процессы	1,50
Существующие процессы при наличии тре­бо­ва­ний по безо­пас­нос­ти, прочности, а также для кри­ти­ческих параметров су­щест­вую­щих про­цес­сов	1,50
Новые процессы при наличии тре­бо­ва­ний по безо­пас­ности, проч­нос­ти, а также для кри­ти­ческих параметров новых про­цес­сов	1,67
Новые процессы (автомобильная промышленность США)	1,67
Новые процессы (Япония)	2,00

НГД

ВГД

Номинал

В интервале от -3 до 3 находится 99.73% значений рассматриваемой величины

Р ис. 6.3. К определению индекса воспроизводимости процесса

Для случая, показанного на рис. 6.3, C_P = 6 / 6 = 1.

Сгла­жен­ная гисто­грам­ма распределения параметра процесса целиком заполняет по­ле допуска, од­нако в этом случае имеется опасение, что появятся де­фект­ные изделия.

Какова их доля? В соответствии с правилом трех сигм, в ин­тервале от ‑3 до +3 около среднего значения _X параметра X находится P = 99,73% из­де­лий, значит при индексе C_P = 1 доля брака составит (1 ‑ P) = 1 ‑ 99,73 % = 0,27 %.