4. Схема исикавы

предназначена для изучения причинно-следственных связей, факторов, влияющих на объект анализа.

Вве­дена в МС ИСО 9004-4: 94.

Для поиска причин, влияющих на конечный результат, часто ис­поль­зу­ют метод мозгового штурма - метод быстрого беспрепятственного ге­не­ри­ро­ва­ния новых идей, когда наилучшее решение не очевидно. Ос­нов­ны­ми пра­ви­ла­ми проведения сессии мозгового штурма являются следующие.

1. Генерируйте большое число идей.

2. Поощряются любые отклонения.

3. Не критикуйте.

4. Стимулируйте участие всех.

5. Записывайте все идеи.

6. Пусть идеи созреют.

7. Подбирайте подходящее место для сессии.

8. Число участников.

Причина

Главная причина уровня 2

Главная причина В

А Причина

уровня 1

Причина

уровня 3

Проблема, подлежащая

решению (результат)

Главная причина Главная причина

С D

Рис. 4.1. Схема построения

диаграммы причинно-следственных связей

Р ис. 4.2. Причинно-следственные связи показателя “Качество восстановления втулки шпинтона” (Схема Исикава)

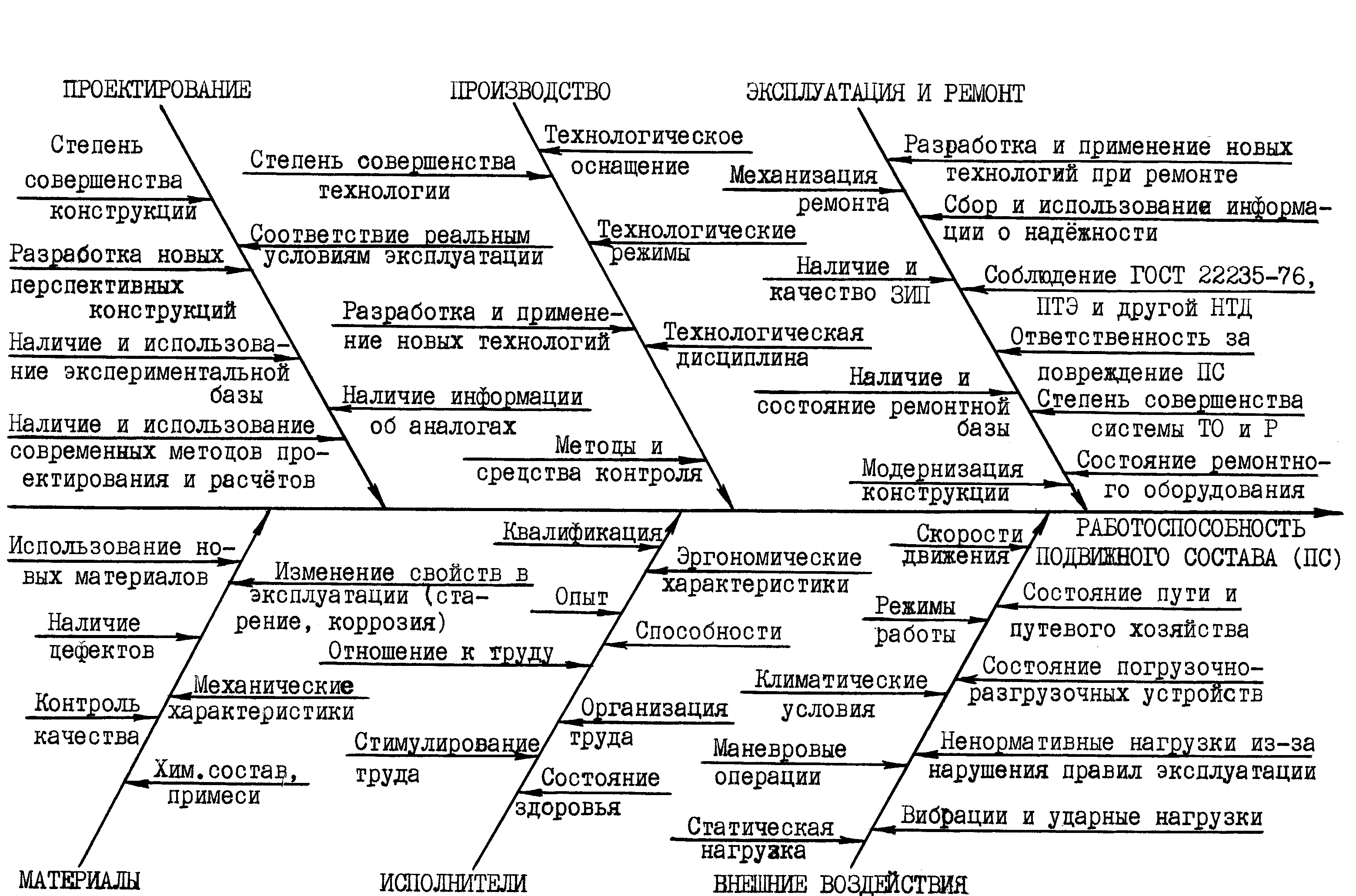
Рис. 4.3. Причинно-следственные связи показателя “Работоспособность подвижного состава”

5. Диаграмма рассеивания

- это инструмент, позволяющий определить вид и тес­ноту связи между парами соответствующих переменных.

Эти две пе­ре­мен­ные могут относиться к:

а) показателю качества и влияющему на него фактору;

б) двум различным показателям качества;

в) двум факторам, вли­я­ю­щим на один показатель качества.

Для выявления связи между ними служит диа­грамма рассеивания, ко­то­рую называют также диаграммой разброса или полем корреляции.

По­сле­до­ва­тель­ность построение ди­аг­рам­мы рас­сеи­ва­ния:

Шаг 1. Выбор переменных (факторов) для анализа.

Шаг 2. Сбор парных данных (x, y), между которыми иссле­ду­ет­ся за­ви­си­мость.

Шаг 3. Построение осей и выбор шкал.

Шаг 4. Построение графика (нанесение пар данных).

Шаг 5. Сделайте на диаграмме все необходимые подписи и обоз­начения (на­звание диаграммы, интервал времени, число n пар дан­ных, названия и еди­­ни­цы измерения для осей, имя человека, пост­роившего диаграмму и т.д.).

Пример 5.

Таблица 5.1.

Данные о давлении воздуха и доле дефектов изделий в рабочие дни

Дата	Давление, кПа	Доля дефектов, %	Дата	Давление, кПа	Доля дефектов, %
1.07.02	0,86	0,889	22.07.02	0,87	0,892
2.07.02	0,89	0,884	23.07.02	0,85	0,877
3.07.02	0,88	0,874	24.07.02	0,92	0,885
4.07.02	0,88	0,891	25.07.02	0,85	0,886
5.07.02	0,84	0,874	26.07.02	0,83	0,896
8.07.02	0,87	0,886	29.07.02	0,87	0,896
9.07.02	0,92	0,911	30.07.02	0,93	0,928
10.07.02	0,86	0,912	31.07.02	0,89	0,886
11.07.02	0,92	0,895	1.08.02	0,89	0,908
12.07.02	0,87	0,896	2.08.02	0,83	0,881
15.07.02	0,84	0,894	5.08.02	0,87	0,882
16.07.02	0,82	0,864	6.08.02	0,89	0,904
17.07.02	0,92	0,922	7.08.02	0,87	0,912
18.07.02	0,87	0,909	8.08.02	0,91	0,925
19.07.02	0,94	0,905	9.08.02	0,87	0,872

Доля дефектов, % n = 30

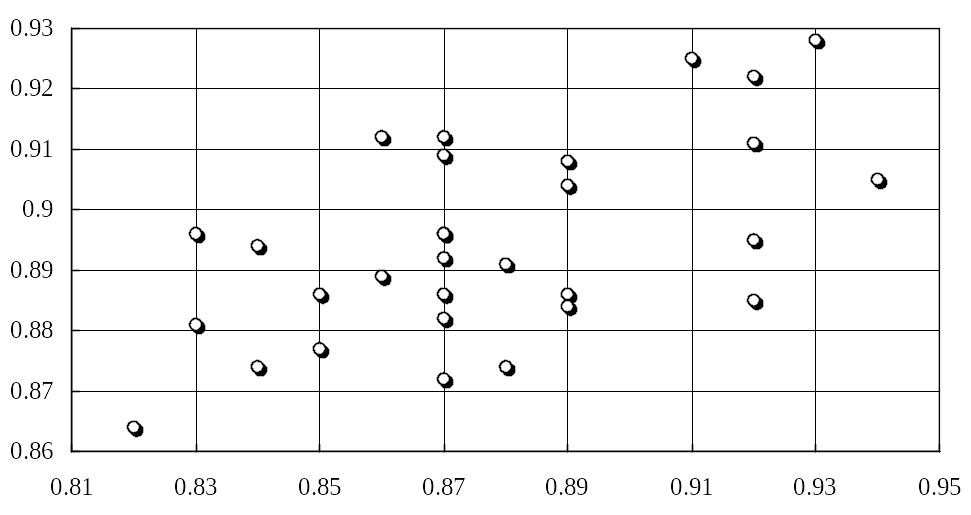
Давление сжатого воздуха, кПа

Рис. 5.1. Диаграмма рассеивания для давления воздуха и доли дефектов

(r = 0,577)

Варианты скопления точек на диаграммах рас­сеи­ва­ния:

положительная (прямая) корреляция величин x и y (рис. 5.2а, б);

отрицательная (об­рат­ная) корреляция (рис. 5.2, в, г);

сильная кор­ре­ля­ции (рис. 5.2, а, в);

слабая кор­ре­ля­ция (рис. 5.2, б, г);

отсутствие кор­ре­ля­ции (рис. 5.2, д);

криволинейная кор­ре­­ляция (рис. 5.2, е).

Расчет коэффициента корреляции r

с ис­поль­зо­ванием па­ке­та анализа MS Excel:

1. Выберите в пункте Сервис (Tools) главного меню Excel команду Анализ данных (Data Analysis).

2. В окне диалога выберите имя необходимого инструмента, например, Корреляция (Correlation) и нажмите кнопку OK.

3. Заполните от­крыв­шееся окно диалога.

а) r  +0,9 б) r  +0,6

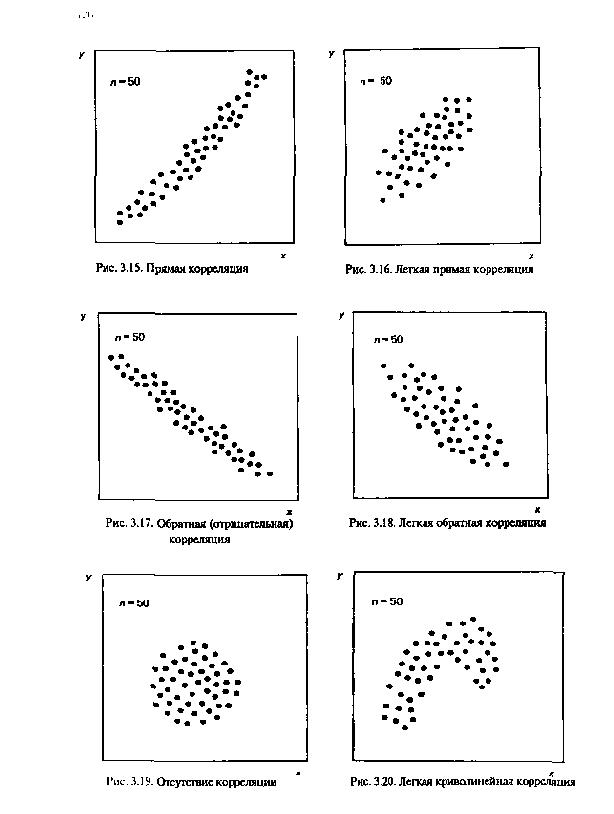
в) r  -0,9 г) r  -0,6

д) r  0 е)

Рис. 5.2. Типичные варианты диаграмм рассеивания

Пример использования диаграммы рассеивания для определения зависимости между пробоем изоляции якоря ТЭД и температурой сушки после пропитки

Анализ ситуации в одном из локомотивных депо Сверд­лов­с­кой ж.д. показал, что число браков из-за выхода из строя тяговых элект­родвигателей (ТЭД) составляет 50% от общего числа браков (16 против 32 случаев), число неплановых ремонтов по ТЭД состав­ля­ет 30,3 % от всех случаев.

При анализе дефектов ТЭД в 2002 г. при испытании в часовом ре­жиме на испытательной станции выявлено 50 случаев пробоя яко­ря ТЭД.

Возможными причинами возникновения пробоев являются:

- несоблюдение температуры запекания;

- несоблюдение времени запекания;

- низкая изоляционная прочность лака.

Чтобы выяснить, действительно ли существует зависимость меж­ду количеством пробоев якоря и указанными факторами, при­ня­то решение провести проверку путем построения диаграммы рассеивания. Для проверки выбрана зависимость между долей воз­ник­ших дефектов и температурой запекания. Для построения диаг­рам­мы рассеивания собраны данные о температуре запекания и чис­ле пробоев, представленные в табл. 5.2. По этим данным пост­рое­на диаграмма рассеивания, представленная на рис. 5.3.

Видно, что переменная Y имеет тенденцию к резкому умень­ше­нию с ростом величины X, следовательно, мы имеем случай силь­ной отрицательной корреляции. Для количественной оценки си­лы связи между значениями X и Y определяем коэффициент кор­ре­ляции, с помощью ПК MS Excel. Коэффициент корреляции сос­та­вил r = – 0,83. То есть, осуществляя контроль над фактором X, мож­но управлять параметром качества Y. Другими словами, из полу­чен­ной диаграммы можно сделать следующий вывод: контролируя тем­пературу запекания, мы можем снизить количество пробоев яко­ря. Оптимальный диапазон температур согласно диаграмме от 128 до 130 ^оС.

Для снижения числа пробоев якоря тягового двигателя ТЛ2К1 необ­ходимо исключить человеческий фактор - поддержание темпера­туры в печах для запекания якорей после пропитки произво­ди­лось в ручном режиме путем включения-выключения нагре­ва­тель­ных элементов. Автоматизация управления температурой в пе­чи в пределах от 129,5 до 130,5 ^оС позволяет исключить пробои, воз­никающие из-за несоблюдения температуры запекания.

Таблица 5.2

Данные о температуре запекания и доле дефектов

Температура, оС	Доля дефектов, %		Температура, оС	Доля дефектов, %
114	0,4		125	0,3
118	0,3		129	0,2
116	0,4		130	0,1
115	0,4		131	0,1
117	0,4		128	0,1
120	0,3		132	0,1
122	0,3		133	0,1
123	0,2		135	0,1
124	0,2		140	0,2
127	0,2		137	0,1
126	0,4		138	0,1

Рис. 5.3. Диаграмма рассеивания

для температуры запекания и доли дефектов

Учет фактора времени -

диаг­рамма рас­сеивания с временным лагом

В некоторых случаях, кроме набора пар значений исследуемых пе­ре­мен­ных (x₁, y₁), (x₂, y₂), …, (x_n, y_n), имеется также информация о периодических мо­ментах времени t₁, t₂, …, t_n, как показано в табл. 5.3. Тогда при проведении ана­лиза появляется возможность учесть фактор времени. Для этого строят диаграм­му рассеивания, смещая значения переменной y относительно фак­то­ра x: (x₁, y₂), (x₂, y₃), …, (x_n-1, y_n), (x_n, y_n+1)^*. Полученный график называют диаг­раммой рас­сеивания с временным лагом (t₂ ‑ t₁). Временной лаг - это сдвиг по вре­мени меж­ду значениями переменных x и y. Аналогично могут быть по­строены диаграммы рассеивания с временным лагом (t₃ ‑ t₁), (t₄ ‑ t₁) и т.д. В не­которых слу­чаях переменные x и y лучше коррелируют между собой при на­личии того или иного временного лага. Целью подобного анализа яв­ля­ется оцен­ка ве­ли­чи­ны временного лага, при котором достигается наи­выс­шая кор­ре­ляция меж­ду показателем качества y и влияющим фактором x.

Таблица 5.3.

Набор данных с учетом фактора времени

Время	t1	t2	t3	…	tn-1	tn
x	x1	x2	x3	…	xn-1	xn
y	y1	y2	y3	…	yn-1	yn

Пример 6. Поставщиками компании-потребителя, занимаю­щей­ся сборкой из­де­лий, являются два завода, которые изготовляют од­но­типные детали двух мо­де­лей: 1 и 2. Введем обозначения: x - чис­ло рекламаций на деталь модели 1; y - число рекламаций на деталь мо­дели 2. Распределение числа рекламаций по ме­ся­цам пред­став­ле­но в табл. 5.4. С использованием про­грам­м (MS Excel, Statistica и т.п.) построить диаграмму рас­сеи­ва­ния, сде­лать вывод о наличии или отсутствии корреляции между чис­лом ре­кла­ма­ций по деталям моделей 1 и 2. Подтвердить сде­лан­ный вывод путем вы­чис­ле­ния коэффициента корреляции r.

Пример 7. Построить диаграммы рассеивания для данных табл. 5.4 с вре­мен­ным лагом 1, 2 и 3 месяца. Путем сравнения диаг­рамм определить, при каком вре­менном лаге достигается наи­выс­шая корреляция между числом рек­ла­ма­ций на детали моделей 1 и 2. Рас­считать коэффициенты корреляции для всех ди­аграмм рас­сеи­ва­ния. Проанализировать полученные результаты.

Таблица 5.4.

Исходные данные к примерам 6 и 7

Распределение числа рекламаций на детали моделей 1 (x) и 2 (y) по месяцам
Месяц	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
x	105	102	100	108	112	115	118	116	120	125	125	128
y	68	71	69	66	65	70	75	76	78	77	79	82