Значения валового объёма Cushair Designs
Период продаж |
Объём розничной продажи, тыс. ф. ст. |
Январь-март 1988 Апрель-июнь 1988 Июль-сентябрь 1988 Октябрь-декабрь 1988 Январь-март 1989 Апрель-июнь 1989 Июль-сентябрь 1989 Октябрь-декабрь 1989 Январь-март 1990 Апрель-июнь 1990 |
278 321 328 364 340 382 369 440 401 417 |
Консультант по менеджменту дал также некоторые рекомендации по поводу того, как можно избежать расчета индексов сезонности для универмага. Он счел эту процедуру нецелесообразной, поскольку в его распоряжении было слишком мало информации за прошлые периоды. Он решил использовать национальный поквартальный индекс сезонности, значения которого публикуются в прессе. Он предполагал, что ассортиментный набор мебельного магазина его клиента незначительно отличается от того ассортиментного набора, на основе которого строится национальный индекс.
|
Январь-март |
Апрель-июнь |
Июль-сентябрь |
Октябрь-декабрь |
Мультипликативный индекс сезонности |
94 |
98 |
96 |
112 |
Требуется:
а) Нанести на график фактические значения квартальных объемов продаж и объяснить, почему мультипликативная модель соответствует этим данным в большей степени, чем аддитивная.
б) Найти значения десезонализированных данных и нанести их на график.
в) Используя метод наименьших квадратов, определить параметры уравнения прямой, проходящей через десезонализированные данные.
г) Рассчитать оценки валового объема продаж в третьем и четвертом кварталах 1990 года.
д) Определить вероятную точность полученных оценок.
Решение:
Построение диаграммы временного ряда:
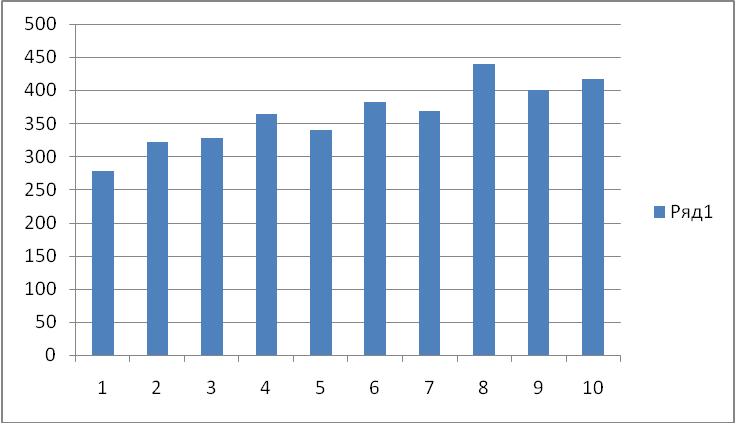
Рис.1 Фактический объём розничных продаж компании.
Объем продаж в 4 кварталах года превышают объемы розничных продаж других кварталов. Что говорит о возрастающем тренде.
2). Анализ модели с мультипликативной компонентой: A = T * S * E
Аддитивная модель представляется как
Фактическое значение = Трендовое значение * Сезонная вариация * Ошибка, т.е.
A = T * S * E.
2.1 Расчет сезонной компоненты методом скользящей средней (S).
Чтобы найти центрированную скользящую среднюю ищем её как средне двух соседних скользящих средних.
Таблица1 Расчёт значений сезонной компоненты
Дата |
Номер квартала |
Объём продаж, тыс. шт. |
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированная скользящая средняя |
Коэффициент сезонности A/T = SxE |
Январь - март 1988 |
1 |
278 |
|
|
|
|
Апрель - июнь |
2 |
321 |
|
|
|
|
|
|
|
1291 |
322,75 |
|
|
Июль - сентябрь |
3 |
328 |
|
|
330,50 |
0,992 |
|
|
|
1353 |
338,25 |
|
|
Октябрь - декабрь |
4 |
364 |
|
|
345,88 |
1,052 |
|
|
|
1414 |
353,5 |
|
|
Январь - март 1989 |
5 |
340 |
|
|
358,63 |
0,948 |
|
|
|
1455 |
363,75 |
|
|
Апрель - июнь |
6 |
382 |
|
|
373,25 |
1,023 |
|
|
|
1531 |
382,75 |
|
|
Июль - сентябрь |
7 |
369 |
|
|
390,38 |
0,945 |
|
|
|
1592 |
398 |
|
|
Октябрь - декабрь |
8 |
440 |
|
|
402,38 |
1,094 |
|
|
|
1627 |
406,75 |
|
|
Январь - март 1990 |
9 |
401 |
|
|
|
|
Апрель - июнь |
10 |
417 |
|
|
|
|
Таким образом, получили десезонализированную среднюю за каждый квартал (кроме 2-х начальных и конечных).
Найдем средние значения сезонных оценок для каждого сезона года. Скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы общая их сумма была равна четырем. Так как значения сезонной компоненты – это доли, а число сезонов равно 4, необходимо, чтобы их сумма была равна 4. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год.
Таблица 2
|
Год |
Номер квартала |
|
|||
|
|
1 |
2 |
3 |
4 |
|
|
1988 |
- |
- |
0,99 |
1,05 |
|
|
1989 |
0,95 |
1,02 |
0,95 |
1,09 |
|
|
1990 |
- |
- |
- |
- |
|
Итого |
0,95 |
1,02 |
1,94 |
2,15 |
Сумма |
|
Оценка сезонной компоненты |
0,95 |
1,02 |
0,97 |
1,07 |
4,013 |
|
Скорректированная сезонная компонента* |
0,94 |
1,02 |
0,97 |
1,07 |
4,000 |
|
2.2. Десезонализация данных при расчете тренда
После того как оценки сезонной компоненты определены, можем приступить к процедуре десезонализации данных по формуле A/S = T х E, что позволяет найти оценки трендовых значений.
Таблица 3 Расчёт десезонализированных данных
Дата |
Номер квартала |
Объём продаж, тыс. шт. A |
Коэффициент сезонности S |
Десезонализированный объём продаж, тыс. шт. A/T = S x E |
Январь - март 1988 |
1 |
278 |
0,94 |
294,2 |
Апрель - июнь |
2 |
321 |
1,02 |
314,7 |
Июль - сентябрь |
3 |
328 |
0,97 |
339,7 |
Октябрь - декабрь |
4 |
364 |
1,07 |
340,4 |
|
|
|
|
|
Январь - март 1989 |
5 |
340 |
0,94 |
359,8 |
Апрель - июнь |
6 |
382 |
1,02 |
374,5 |
Июль - сентябрь |
7 |
369 |
0,97 |
382,1 |
Октябрь - декабрь |
8 |
440 |
1,07 |
411,4 |
|
|
|
|
|
Январь - март 1990 |
9 |
401 |
0,94 |
424,4 |
Апрель - июнь |
10 |
417 |
1,02 |
408,8 |
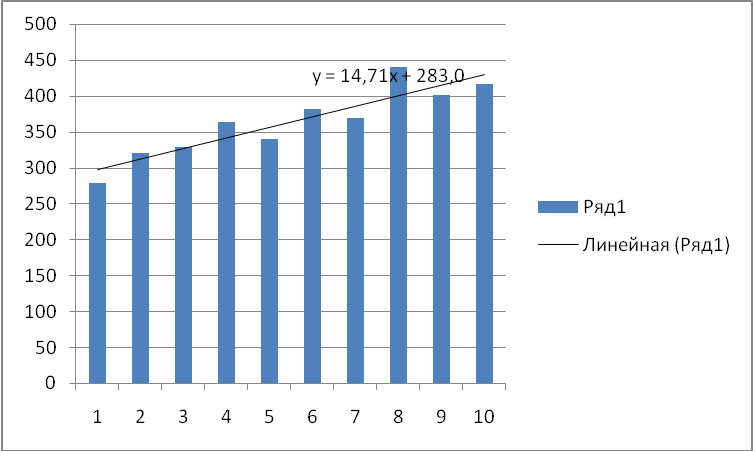
Очевидно, что линия тренда – не кривая, а прямая. Из диаграммы видно, что наши десезонолизированные данные имеют линейный вид, поэтому мы можем применить линейный тренд.
2.3. Оценка значений тренда.
T = a + b х – номер квартала, где x – порядковый номер квартала, y – значение (T * E) в предыдущей таблице, a и b характеризуют точку пересечения с осью ординат и наклон линии тренда.
,
,
b= 14,71
a= 283,06
Трендовое значение объема продаж: Т = 283,06+14,71х
2.4. Расчет ошибок или остатка.
Вычитая из фактического товарооборота значения тренда и сезонной составляющей можно найти значения ошибок.
Таблица 4
Дата |
Номер квартала |
Объём продаж, тыс. шт. A |
Сезонная компонента S |
Трендовое значение, тыс. шт. Т |
Ошибка |
||
|
|
|
|
|
TxS |
A/(TxS) |
A - (TxS) |
Январь - март 1988 |
1 |
278 |
0,94 |
297,8 |
281,4 |
0,99 |
-3,4 |
Апрель - июнь |
2 |
321 |
1,02 |
312,5 |
318,8 |
1,01 |
2,2 |
Июль - сентябрь |
3 |
328 |
0,966 |
327,2 |
316,0 |
1,04 |
12,0 |
Октябрь - декабрь |
4 |
364 |
1,07 |
341,9 |
365,7 |
1,00 |
-1,7 |
|
|
|
|
|
|
|
|
Январь - март 1989 |
5 |
340 |
0,94 |
356,6 |
337,0 |
1,01 |
3,0 |
Апрель - июнь |
6 |
382 |
1,02 |
371,4 |
378,8 |
1,01 |
3,2 |
Июль - сентябрь |
7 |
369 |
0,966 |
386,1 |
372,8 |
0,99 |
-3,8 |
Октябрь - декабрь |
8 |
440 |
1,07 |
400,8 |
428,6 |
1,03 |
11,4 |
|
|
|
|
|
|
|
|
Январь - март 1990 |
9 |
401 |
0,94 |
415,5 |
392,6 |
1,02 |
8,4 |
Апрель - июнь |
10 |
417 |
1,02 |
430,2 |
438,8 |
0,95 |
-21,8 |
Полученные данные можно использовать при расчете среднего абсолютного отклонения (MAD) или средней квадратической ошибки (MSE):
1)
MAD=16
2)
MSE=35
Вывод:
Построенная модель совпадает с фактическими данными, поскольку ошибка Е не превышает 5%
