Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Санкт-петербургский государственный университет аэрокосмического приборостроения»

РУКОВОДИТЕЛЬ

асс.				Морозов С.А.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторные работы на тему: Мультипликативная модель

по дисциплине: Прогнозирование в условиях рынка

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.	Z8M52K				Пирогов Д.Г.
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2013

Упражнение 2.1

Положение дел в компании «Doble-Flood» достаточно тяжелое. Ниже приводятся данные о прибыли компании за последние 10 кварталов (скорректированные на инфляцию).

Год	1	2	3
Квартал	1 2 3 4	1 2 3 4	1 2
Прибыль	146 106 123 89	97 74 80 53	56 35

Требуется:

1. Построить модель временного ряда с мультипликативной компонентой.

2. Дать прогноз на два следующих квартала года 3.

Решение:

1. Построение диаграммы временного ряда:

товарооборот компании за последние 10 кварталов

Дата	Номер квартала	Объём продаж, тыс. шт. A
Январь - март 2009	1	137
Апрель - июнь	2	102
Июль - сентябрь	3	113
Октябрь - декабрь	4	93
Январь - март 2010	5	92
Апрель - июнь	6	77
Июль - сентябрь	7	85
Октябрь - декабрь	8	51
Январь - март 2011	9	59
Апрель - июнь	10	38

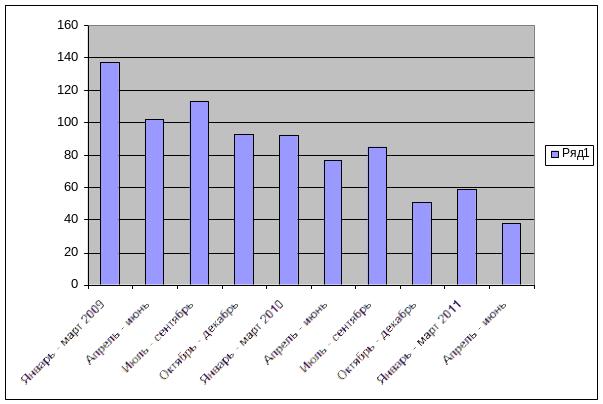
Рис1: Диаграмма временного ряда

2). Анализ модели с мультипликативной компонентой: A = T х S х E

В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения. Таким образом, значения сезонной компоненты увеличиваются с возрастанием значений тренда.

модель с мультипликативной компонентой представляется как:

Фактическое значение = Трендовое значение х Сезонная вариация х Ошибка,

т.е.

A = T х S х E.

2.1 Расчет сезонной компоненты методом скользящей средней (S).

Чтобы найти центрированную скользящую среднюю ищем её как средне двух соседних скользящих средних. А оценки сезонной компоненты представляют собой коэффициенты, полученные по формуле А/Т = S х E. Результаты расчетов приведены в таблице 2.

Таблица 2. Расчёт по 4 точкам центрированных скользящих средних значений тренда для модели

А/Т = S х E.

Дата	товарооборот	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты А/Т = S х E.
Январь - март 2009	137
Апрель - июнь	102
		445	111,25
Июль - сентябрь	113			105,625	1,070
		400	100
Октябрь - декабрь	93			96,875	0,960
		375	93,75
Январь - март 2010	92			90,25	1,019
		347	86,75
Апрель - июнь	77			81,5	0,945
		305	76,25
Июль - сентябрь	85			72,125	1,179
		272	68
Октябрь - декабрь	51			63,125	0,808
		233	58,25
Январь - март 2011	59			47,625	1,239
		148	37
Апрель - июнь	38

Таким образом, получили десезонализированную среднюю за каждый квартал (кроме 2-х начальных и конечных).

Найдем средние значения сезонных оценок для каждого сезона года. Так как значения сезонной компоненты – это доли, а число сезонов равно 4, необходимо, чтобы их сумма была равна 4. Если эта сумма не равна четырем, производится корректировка значений сезонной компоненты точно таким же образом, как это уже делалось ранее.

Сумма/4=0,97

Таблица 3.

Год	Номер квартала
	1	2	3	4
2009			1,07	0,96
2010	1,019	0,945	1,179	0,808
2011	1,239
Итого	2,258	0,945	2,249	1,768	Сумма
Оценка сезонной компоненты	1,13	0,95	1,12	0,88	4,08
Скорректированная сезонная компонента*	1,106	0,926	1,102	0,866	4,000

2.2. Десезонализация данных и расчет уравнения тренда

После того как оценки сезонной компоненты определены, можем приступить к процедуре десезонализации данных по формуле A/S = T х E.

Таблица 4.

Дата	квартал	Объём товарооборота, тыс. A	Сезонная компонента S	Десезонализированный объём продаж, тыс. шт. A/S = T x E
Январь - март 2009	1	137	1,106	123,9
Апрель - июнь	2	102	0,926	110,2
Июль - сентябрь	3	113	1,102	102,5
Октябрь - декабрь	4	93	0,866	107,4
Январь - март 2010	5	92	1,106	83,2
Апрель - июнь	6	77	0,926	83,2
Июль - сентябрь	7	85	1,102	77,1
Октябрь - декабрь	8	51	0,866	58,9
Январь - март 2011	9	59	1,106	53,3
Апрель - июнь	10	38	0,926	41,0

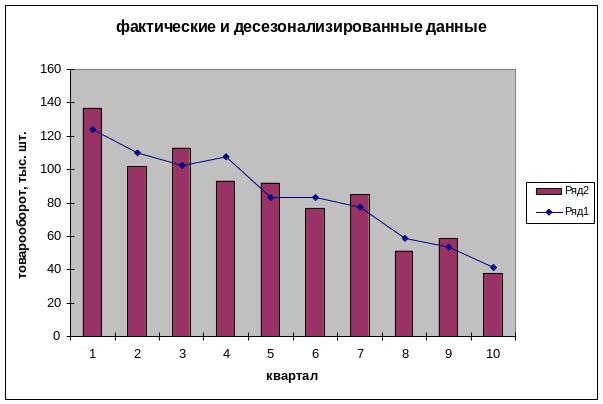
Рис.2. Фактический и десезонализирванный товарооборот.

Гистограмма с линией тренда ОХ – квартал, ОУ товарооборот. Линия тренда – оценка.

2.3. Оценка значений тренда.

Теперь нужно принять решение о том, какой вид будет иметь уравнение тренда. Очевидно, что линия тренда – не кривая, наоборот, она несколько больше напоминает прямую, хотя отдельные точки, особенно значения за 2009 г., расположены хаотически. Предположим для простоты, что тренд линейный, и для расчета параметров прямой, наилучшим образом его аппроксимирующей, будем применять метод наименьших квадратов.

T = a + b х – номер квартала, где x – порядковый номер квартала, y – значение (T + E) в предыдущей таблице. находим, что

Т = 132,5 -8,8 х

,

,

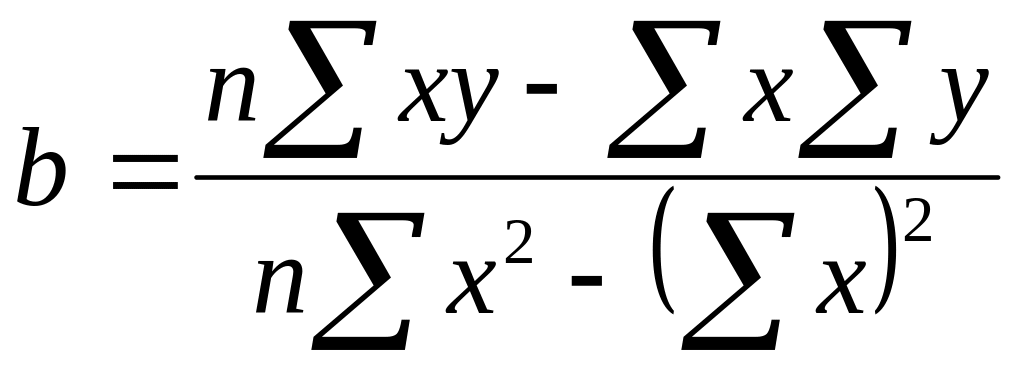b=-8,8

a=132,476

Это уравнение будем использовать в дальнейшем для расчета оценок трендовых объемов продаж на каждый момент времени.

2.4. Расчет ошибок: A/(T х S) = E или A – (T х S) = E

Итак, мы нашли значения тренда и сезонной компоненты. Теперь мы можем использовать их для того, чтобы рассчитать ошибки в прогнозируемых по модели объемов продаж Т х S по сравнению с фактическими значениями А. В таблице 5. эти ошибки рассчитаны как отношение Е = А/(Т х S).

Таблица 5.

Дата	квартал	Объём товарооборота, тыс. A	Сезонная компонента S	Десезонализированный объём продаж, тыс. шт. A/S = T x E	Трендовое значение, тыс. шт. Т	Ошибка
						TxS	A/(TxS)	A - (TxS)
Январь - март 2009	1	137	1,106	123,9	123,7	136,8	1,00	0,2
Апрель - июнь	2	102	0,926	110,2	114,9	106,4	0,96	-4,4
Июль - сентябрь	3	113	1,102	102,5	106,1	116,9	0,97	-3,9
Октябрь - декабрь	4	93	0,866	107,4	97,3	84,2	1,10	8,8
Январь - март 2010	5	92	1,106	83,2	88,5	97,9	0,94	-5,9
Апрель - июнь	6	77	0,926	83,2	79,7	73,8	1,04	3,2
Июль - сентябрь	7	85	1,102	77,1	70,9	78,1	1,09	6,9
Октябрь - декабрь	8	51	0,866	58,9	62,1	53,8	0,95	-2,8
Январь - март 2011	9	59	1,106	53,3	53,3	58,9	1,00	0,1
Апрель - июнь	10	38	0,926	41,0	44,5	41,2	0,92	-3,2

2.5. Прогнозирование по модели с мультипликативной компонентой

При составлении прогнозов по любой модели предполагается, что можно найти уравнение, удовлетворительно описывающее значения тренда. В обоих изложенных выше примерах эта предпосылка была успешно выполнена. Тренд, который нами рассматривался, был очевидно линейным. Если бы исследуемый тренд представлял собой кривую, мы были бы вынуждены моделировать эту связь с помощью одного из методов формализации нелинейных взаимосвязей, рассмотренных в предыдущей главе. После того как параметры уравнения тренда определены, процедура составления прогнозов становится совершенно очевидной. Прогнозные значения определяются по формуле:

F = T х S,

где

T = 132,5 -8,8 х номер квартала ( тыс. шт. за квартал),

а сезонные компоненты составляют 1,106 в первом квартале, 0,926 – во втором, 1,102 – в третьем и 0,866 в четвертом квартале. Ближайший следующий квартал – это третий квартал 2011 г., охватывающий период с Июля по сентябрь имеющий во временном ряду порядковый номер 11. Прогноз объема продаж в этом квартале составляет:

F = T х S = (132,5 -8,8 х 11) х 1,106 = 39,5(тыс. шт. за квартал).

Аналогично, прогноз на октябрь- декабрь 2011 г., рассчитывается для квартала с порядковым номером 12 с использованием значения сезонной компоненты для IV квартала года:

F = T х S = (132,5 -8,8 х 12) х 0,866 = 23,3 (тыс. шт. за квартал).

Разумно предположить, что величина ошибки данного прогноза будет несколько выше, чем предыдущего, поскольку этот прогноз рассчитан на более длительную перспективу.

Вывод: С каждым новым кварталом предприятие получает все меньше прибыли, что может привести к полному банкротству.

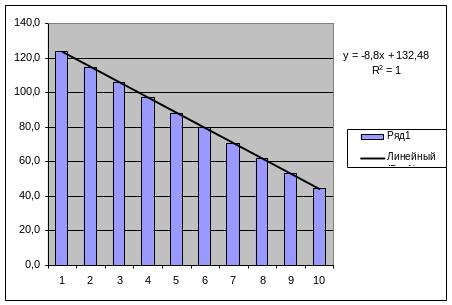
Рисунок 4 – Линейный тред

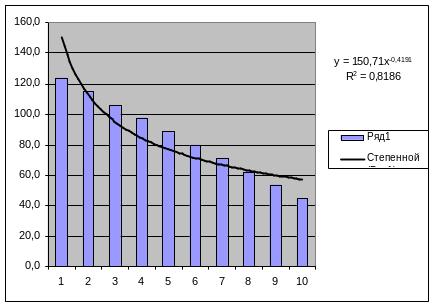
Рисунок 5 - степенной тренд

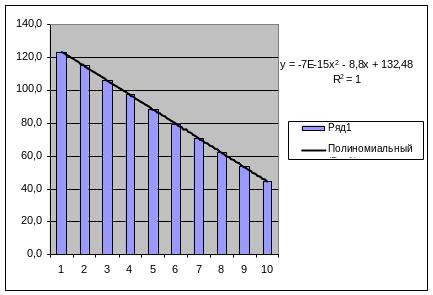
Рисунок 6 - полиномиальный тренд

Вывод: нашей модели соответствует полиномиальный тренд и линейный, т.к. R² = 1 и они максимально приближены к 1 из всех построенных.

1.Линейная регрессия и оценка ее параметров.

Ранее было найдено, что b= -8,8 , a = 132,5

Получаем y= 132,5-8,8х

Вывод: Так как коэффициент а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. А это значит, что с увеличением квартала – х , прибыль будет уменьшаться в среднем на 8,8 тыс.руб.

2.Коэффициент корреляции (r_xy):

b= -8,8- коэффициент регрессии

r_xy =-0,98

Вывод: Так как r_xy < 0 , значит объем продаж с каждым кварталом имеет тенденцию к убыванию, т.е. чем больше квартал тем меньше прибыль, т.е. имеем сильную отрицательную зависимость.

1).Т.к. коэффициент регрессии (b=-8,8) и b <0, то это значит, что прибыль будет уменьшаться при неизменном уровне предыдущего значения уровня продаж .

2). Т.к. коэффициент корреляции близок к -1 (r_xy =-0,95), то мы имеем прямо-пропорциональную зависимость между нашими параметрами.

3.Коэффициент детерминации:

R² = (-0,98)² = 0,9604

Вывод: Т.к. коэффициент детерминации (R² = 0,9604)очень близок к 1, то в построенной модели 96,04 % изменение прибыли объясняется изменением номера квартала.

4. Средняя ошибка аппроксимации:

=72,05

=1/10*0.123*100% = 1,23%

А= 1,23 %

Вывод: Т.к. Средняя ошибка аппроксимации <10% , то достоверность построенной модели высока, в среднем расчетное значение отклоняются от фактических на 1,23%

5.Эластичность:

Э=3,31*0,158.= -0,57%

Вывод: на 0,57 % в среднем изменится по совокупности прибыль от своей средней величины при изменении временных кварталов на 1 % от своей средней величины.

Упражнение 2.2

Объемы выпуска компании «Banham and Barsey» возрастают из года в год. Ниже приведены значения этого показателя.

Год	1	2	3
Квартал	2 3 4	1 2 3 4	1 2 3
Объем выпуска	400 715 600	585 560 975 800	765 720 1235

Требуется:

1. Построить соответствующую модель временного ряда с мультипликативной компонентой.

2. Дать прогноз на два следующие квартала.

Решение: