Лекція № 4

Тема: Рівняння ліній другого порядку

План

1. Загальне рівняння ліній другого порядку

2. Коло

3. Еліпс

4. Гіпербола

5. Парабола

Література:

Основна:

1. Грисенко М.В.. Математика для економістів: Методи й моделі, приклади й задачі: Навч. посібник. – К.: Либідь, 2007. – 720с.

2. Клепко Ю.В., Голець В.Л. Вища математика в прикладах і задачах: Навчальний посібник. – К.: Центр навчальної літератури, 2006.

3. Дубовик В.П., Юрик І.І.. Вища математика: Навч. посібник. – К.: А.С.К., 2001.- 648с.: іл..

Додаткова:

1. Кудрявцев В.А., Демидович Б.П.. Краткий курс высшей математики. М., Физматгиз, 1962г., 528 стр. с илл.

2. Гаврильченко Х.І., Полушкін С.П., Кропив’янський П.С. та ін.. Вища математика: Зб. Задач: У 2 ч. Ч.1: Лінійна і векторна алгебра. Аналітична геометрія. Вступ до математичного аналізу. Диференціальне та інтегральне числення: Навч. посібник для вищ. техн. навч. закл./ За заг.ред. д-ра техн. наук, проф.. Овчинникова. – 2-ге вид., стереотип. – К.: Техніка, 2004. – 279с.: іл..

Зміст лекції

1. Загальне рівняння ліній другого порядку

Лінії, координати двох точок яких задовольняють рівняння, що в прямокутній системі координат є рівнянням другого степеня, називають лініями, або кривими другого порядку. Загальне рівняння лінії другого порядку:

.

До них належать коло, еліпс, гіпербола, парабола.

2. Коло

Означення. Коло — це геометричне місце точок площини, віддалених від фіксованої точки на фіксовану відстань. Фіксовану точку С(х_о ;у_о) називають центром кола, а фіксовану відстань R — радіусом кола.

Виведемо рівняння кола з центром у точці С(х₀ ;у_о) і радіуса R . Нехай М(х;у) — довільна точка кола (рис. 1);

Оскільки CM = R, то CМ² = R ²,

Отже, рівняння кола має вигляд

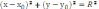(1)

Це рівняння називають канонічним рівнянням кола.

Приклад. Написати рівняння кола, якщо відомо, що А(-6; 4) і В(2; 10) — діаметрально протилежні точки кола.

Розв'язання. Точка С — середина відрізка АВ — буде центром кола. С(-2; 7). Радіус кола дорівнює ВС.

=5

Знаючи центр і радіус кола, за формулою (1) отримуємо рівняння кола (х + 2)² + (у — 7)² = 25.

3. Еліпс

Означення. Еліпс – це геометричне місце точок площини, сума відстаней від яких до двох заданих точок площини є величиною сталою, що перевищує відстань між цими точками.

Дві задані точки F₁ і F₂ називають фокусами еліпса, а відстань F₁F₂ — фокусною відстанню.

Виведемо рівняння еліпса. Нехай М — його довільна (або біжуча) точка. За означенням F₁M+ F₂M= 2 а = const.

Позначимо F₁F₂ = 2с < 2а. Виберемо прямокутну декартову систему координат так, щоб вісь Ох збігалася з прямою F₁F₂, а вісь Оу проходила через середину F₁F₂.Тоді F₁ (-с,0), F₂ (С,0).

; .

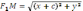За означенням еліпса .

Перенесемо один з коренів у праву частину, піднесемо обидві частини до квадрату і зведемо подібні доданки:

Піднесемо обидві частини до квадрату ще раз: .

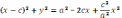Після зведення подібних доданків дістаємо :

Введемо позначення: (нагадаємо, що а > с).

Рівняння набере вигляду

Після ділення обох частин на отримаємо: (2)

Це канонічне рівняння еліпса.

І з рівняння (2) випливає, що еліпс симетричний відносно початку координат, бо координати точок М₁(х,у) і М₂(-х,-у) або водночас задовольняють рівняння (2), або водночас його не задовольняють.

Осі Ох і Оу є осями симетрії еліпса, бо з того, що точка М₁(х,у) належить еліпсу, випливає, що точки М₃(х,-у)) і М₄(-х,у) так само належать еліпсу (рис.З).

Відрізок А_іА₂- велика вісь еліпса (ОА₂, ОА₁ — великі півосі). Відрізок В₁В₂ — мала вісь еліпса (ОВ₁, ОВ₂ — малі півосі). ОскількиF₁В₂+F₂В₂=2а,то

Точки А₁, А₂, В₁, В₂ — вершини еліпса; О — центр еліпса. Можна довести, що еліпс із центром у точці С(х₀ ,у_о) і півосями а і b (а > b), що паралельні осям координат, має таке рівняння: (3)

О значення. Ексцентриситетом еліпса називають число , яке дорівнює відношенню , тобто ,

Очевидно, що . Отже, = 0 тоді і тільки тоді, коли b= а.

У цьому разі еліпс вироджується в коло (фокуси F₁ і F₂ збігаються з центром кола).

При збільшенні ексцентриситету еліпс дедалі сильніше витягується вздовж великої осі.

Означення. Директрисами еліпса називають прямі , які перпендикулярні до великої осі еліпса і розміщуються на відстані від центра еліпса.

Для еліпса ,заданого рівнянням (2), директриси мають рівняння х=± , х= ± , а для еліпса, заданого рівнянням (3),х=х₀ ± . Оскільки , то директриси еліпс не перетинають. Для кола поняття директриси відсутнє (оскільки ).

Приклад. Побудувати еліпс, заданий рівнянням 9х² - 18х + 25у² + 100у -116 =0.

Знайти ексцентриситет, координати фокусів і рівняння директрис . Побудувати фокуси та директриси.

Розв'язання. Виділимо повні квадрати:

9(х² - 2х +1) - 9 + 25 (у² + 4у + 4) -100 -116 = 0.

Звідси :

З рівняння (З) робимо висновок, що це еліпс з центром у точці С(1;-2) і півосями а= 5,b = 3. Фокуси віддалені від центра на відстань с = і лежать на великій осі.

Т ому F₁ (-3;-2); F₂(5; -2).

Ексцентриситет

Директриси d₁ і d₂ віддалені від центра на відстань .

Тому їх рівняння