4. Парабола

Означення. Парабола — це геометричне місце точок площини, відстань від яких до заданої точки дорівнює відстані до заданої прямої, що не проходить через задану точку.

Задану точку і⁷ називають фокусом параболи, а задану пряму сі— директрисою параболи. Відстань від фокуса до директриси називають фокальним параметром параболи і, як правило, позначають р.

Виведемо рівняння параболи. Нехай Н — проекція точки F да директрису сі. Виберемо прямокутну декартову систему координат так, щоб вісь Ох збігалася з прямою Яі⁷, а вісь Оу була серединним перпендикуляром до ЯР (рис. 8). Тоді

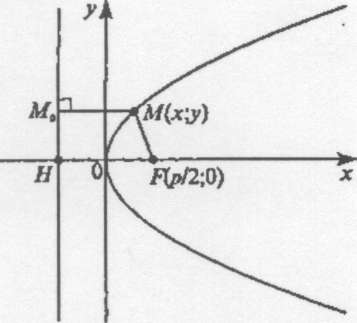
Рис. 8

Нехай М(х; у) — довільна точка параболи, а М₀ — її проекція на директрису. Тоді

За означенням |х + |= +

Піднісши обидві частини до квадрату і звівши подібні доданки, отримаємо канонічне рівняння параболи

/=2рх. (5)

Парабола не має центра симетрії, але вісь Ох є віссю симетрії параболи, оскільки координати точок Му (х;у) і М₂(х;-у) одночасно або задовольняють рівняння (5), або не задовольняють це рівняння.

Точку перетину параболи з її віссю називають вершиною параболи.

Зауваження. У шкільному курсі математики розглядають параболу, вісь якої паралельна осі Оу, У такому разі парабола, яка за формою збігається з параболою (8.9), має рівняння

х = 2ру, або у = — х².

2 р

Отже, звичайна парабола у = х² — це геометричне місце точок площини, відстань від яких до точки і^О; - ) дорівнює відстані до

1

прямої^ =-—.

В аналітичній геометрії зручніше розглядати параболи, задані рівнянням (5).

Якщо парабола має вершину в точці С(х₀,уо) і вісь паралельну осі Ох, то її рівняння

(У-Уо)² = 2р(х-х₀). (6)

Властивість (оптична властивість параболи). Дотична, що проведена через довільну точку М параболи, утворює рівні кути з відрізком ¥М і з віссю параболи (рис. 9).

Ця властивість параболи має надзвичайно широке використання:

1. Усі промені, які йдуть паралельно осі параболи, при відбиванні від параболи проходять через фокус. На цьому ґрунтується принцип дії параболічної антени, яка отримується при обертанні частини параболи навколо осі. Промені, які йдуть паралельним потоком до осі тіла обертання, відбиваючись від його поверхні, потрапляють у фокус, де й розміщують приймальний пристрій.

Рис. 9

2. Усі промені, які виходять з фокуса параболи, відбиваючись від неї, рухаються паралельно осі. На цьому ґрунтується принцип дії потужних авіаційних прожекторів: дзеркало виготовляють у вигляді параболоїда обертання, а потужне джерело світла розташовують у його фокусі. При цьому світлові промені, відбиваючись від поверхні дзеркала, ідуть паралельним пучком, що значно зменшує розсіювання.

Криві другого порядку часто спостерігаються на практиці: тіло, кинуте під кутом до горизонту, летить по параболічній траєкторії; планети рухаються навколо Сонця по еліптичних орбітах, в одному з фокусів якого воно розташоване; усі комети Сонячної системи рухаються або по еліпсу, або по параболі, або по гіперболі (залежно від їх швидкості).

Криві другого порядку використовують для опису закономірностей в економічних та соціологічних процесах.

Цікаво, що еліпс, гіперболу і параболу можна отримати при перетині кругового конуса площиною, що не проходить через його вершину (парабола як проміжна лінія утвориться при перетині площиною, паралельною до деякої твірної конуса). Тому ці лінії часто називають конічними перерізами. Вперше їх повністю дослідив Аполлоній Пергський.

Питання для самоконтролю:

1. .Дайте означення кола.

2. Дайте означення еліпса.

' 3. Дайте означення гіперболи.

4. Дайте означення параболи

5.Запишіть рівняння кола.

6. Запишіть рівняння еліпса.

7. Запишіть рівняння гіперболи.

8. Запишіть рівняння параболи.

9. Що таке ексцентриситет, директриса еліпса ?

10. Що таке ексцентриситет, директриса гіперболи?

1. .Де використовують криві другого порядку економічних та соціологічних

процесах?

Означення. Конічним перерізом називається крива, по якій круговий конус перетинається довільною площиною, що не проходить через його вершину (рис.1).

Рис. 1

Коли зазначена площина перетинає всі твірні конуса, у перерізі утворюється крива , яка називається еліпсом.

Крива , яка утворюється в тому разі, коли площина перерізу паралельна єдиній твірній конуса, називається параболою.

Якщо площина перерізу паралельна двом твірним конуса, відповідна крива  називається гіперболою. При цьому площина перетинає обидві порожнини конуса, тому гіпербола розпадається на дві вітки.

Усі конічні перерізи мають спільні властивості, які полягають ось у чому.

Означення. Кожний конічний переріз, крім кола, являє собою геометричне місце точок площини, відношення відстаней яких від деякої фіксованої точки F, що називається фокусом, і деякої прямої, що називається директрисою, є величина стала. Це так званий ексцентриситет. Позначають його .

При конічний переріз є еліпсом, при — параболою, а при — гіперболою.

Складемо рівняння конічного перерізу в полярних координатах, беручи за фокус полюс. Полярну вісь проведемо перпендикулярно до директриси  (рис. 3.39).

Рис. 3.39

Відстань від фокуса до директриси позначимо р. Відстань d до директриси дорівнює або залежно від того, праворуч чи ліворуч від директриси міститься точка. Тепер записуємо рівняння конічного перерізу

або

(2)

Звідси маємо:

Для еліпса і параболи у формулі (2) береться знак «+», для гіперболи — обидва знаки. На рис. 3.40 зображено конічні перерізи при різних значеннях .

Рис. 3.40

Запишемо рівняння конічних перерізів у декартових координатах. Згідно з (2) маємо:

Узявши до уваги (1), дістанемо:

,

або

(3)

Спростимо запис рівняння при різних значеннях .

1. При  = 1:

Позначивши

прийдемо до канонічного рівняння параболи

(4)

2. При виділимо в рівнянні (3) повний квадрат. Тоді дістанемо рівняння

Узявши нові координати

дістанемо рівняння

або

Для скорочення запису застосуємо позначення:

(5)

Остаточно маємо канонічне рівняння еліпса

(6)

При утворюється канонічне рівняння гіперболи:

(7)