Лекція № 4

Тема: Рівняння ліній другого порядку

План

1. Коло

2. Еліпс

3. Гіпербола

4. Парабола

Література:

1. Грисенко М.В.. Математика для економістів: Методи й моделі, приклади й задачі: Навч. посібник. – К.: Либідь, 2007. – 720с.

2. Клепко Ю.В., Голець В.Л. Вища математика в прикладах і задачах: Навчальний посібник. – К.: Центр навчальної літератури, 2006.

3. Дубовик В.П., Юрик І.І.. Вища математика: Навч. посібник. – К.: А.С.К., 2001.- 648с.: іл..

Зміст лекції

Лінії, координати двох точок яких задовольняють рівняння, що в прямокутній системі координат є рівнянням другого степеня, називають лініями, або кривими, другого порядку. До них належать коло, еліпс, гіпербола, парабола.

Означення. Коло — це геометричне місце точок площини, віддалених від фіксованої точки на фіксовану відстань. Фіксовану точку С(х_о ;у_о) називають центром кола, а фіксовану відстань R — радіусом кола.

Виведемо рівняння кола з центром у точці С(х₀ ;у_о) і радіуса R . Нехай М(х;у) — довільна точка кола (рис. 1);

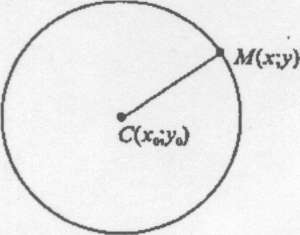Оскільки CM = R, то CМ² = R ²,

Отже, рівняння кола має вигляд

Це рівняння називають канонічним рівнянням кола.

Приклад. Написати рівняння кола, якщо відомо, що А(-6; 4) і В(2; 10) — діаметрально протилежні точки кола.

Розв'язання. Точка С — середина відрізка АВ — буде центром кола. С(-2; 7). Радіус кола дорівнює ВС.

ВС =_л/(-2-2)² + (7-10)² = 5. Знаючи центр і радіус кола, за формулою (1) отримуємо рівняння кола (х + 2)² + (у — 7)² = 25.

випливає, що точки М₃(х,-у)) і М₄(-х,у) так само належить еліпсу (рис.З):

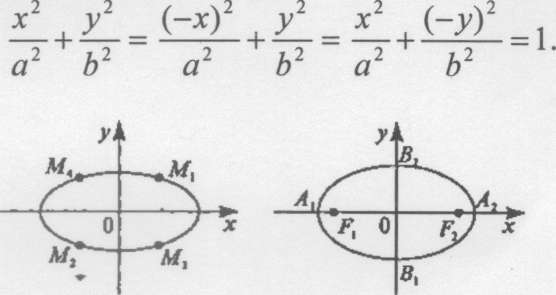
Рис. З

Відрізок А іА₂- велика вісь еліпса (ОА₂, О А_; — великі півосі). Відрізок В,В₂ — мала вісь еліпса (ОВ_и ОВ₂ — малі півосі). Оскільки ГіВ₂+ Р₂В₂— 2а, то

Р,В₂=а; В₂0 = ^Р_хВ²₁-Р_х0² = уІа²-с² = Ь.

Точки Аі, А₂, В], В₂ — вершини еліпса; О — центр еліпса. Можна довести, що еліпс із центром у точці С(х₀ ,уо) і півосями а і Ь (а > Ь), що паралельні осям координат, має таке рівняння:

(*-*<>)* (У-УоУ

= 1. (3)

а' Ь¹

Означення. Ексцентриситетом еліпса називають число є, яке

дорівнює відношенню — , тобто

а

а

Оскільки с = а - b , то є

а

J 2 _l2 _ ліа² -b² Г, І₂

-f-V ■

Очевидно, що 0 <є < 1. Отже,

є = 0 тоді і тільки тоді, коли 6= а, У цьому разі еліпс вироджується в коло (фокуси Fii F₂ збігаються з центром кола).

-1

При збільшенні ексцентриситету еліпс дедалі сильніше витягується вздовж великої осі (put. 4).

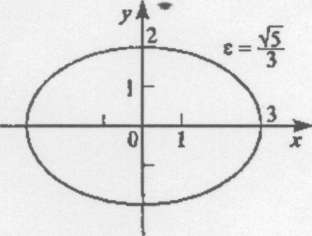
Рис. 4

Означення. Директрисами еліпса називають прямі , які перпендикулярні до

великої осі еліпса і розміщуються на відстані —від центра еліпса.

е

яких до двох здданих точок площини є величиною сталою, що перевищує відстань між цими точками.

Дві задані точки F; і F₂ називають фокусами еліпса, а відстань FjF₂ — фокусною відстанню.

Виведемо рівняння еліпса. Нехай М — його довільна (або біжуча) точка. За означенням FjM+ F₂M= 2 а = const.

F, 0

Позначимо FjF₂ = 2с < 2а. Виберемо прямокутну декартову систему координат так, щоб вісь Ох збігалася з прямою F{F₂, а вісь Оу проходила через середину F,F₂. Тоді F, (-с,0) ,F₂ (С,0)..

уп

.ЩхО')

Л *

Рис. 2

Р₁М = _ЛІ(х + с)²+у² ; уІіх-сУ+у² .

За означенням еліпса

+ у = а—х. а

■УІ(х + с)²+у² +уі(х-с)²+у² = 2а. Перенесемо один з коренів у праву частину, піднесемо обидві частини до квадрату і зведемо подібні доданки:

л/(*-*)² ■ "^а - - ^С

Піднесемо обидві частини до квадрату ще раз:

2

(х-с)² +у² =al-2cx+ ^-г х².

а

Після зведення подібних доданків дістаємо :

2 2

СІ ~ X 2 2 2 2

—я:² + у =а -с.

а

2 2 2

Введемо позначення: а —с =Ь (нагадаємо, що а > с). Рівняння набере вигляду

2 , ,.2 _ іЛ

а

у

Після ділення обох частин на Ь отримаємо:

®

Це канонічне рівняння еліпса.

Із рівняння (2) випливає, що еліпс симетричний відносно початку координат, бо координати точок Мі(х,у) і М₂(-х,-у) або водночас задовольняють рівняння (2), або водночас його не задовольняють.

Осі Ох і Оу є осями симетрії еліпса, бо з того, що точка М₁(х,у) належить еліпсу,

Для еліпса ,заданого рівнянням (^.директриси мають рівняння х=± —,

є

2 2

х= ± —,а для еліпса ,заданого рівнянням (3),х=х₀ ±—.Оскільки 0 <є < 1 , то

с с

директриси еліпс не перетинають. Для кола поняття директриси відсутнє

(оскільки — —>00 при £—>00). є

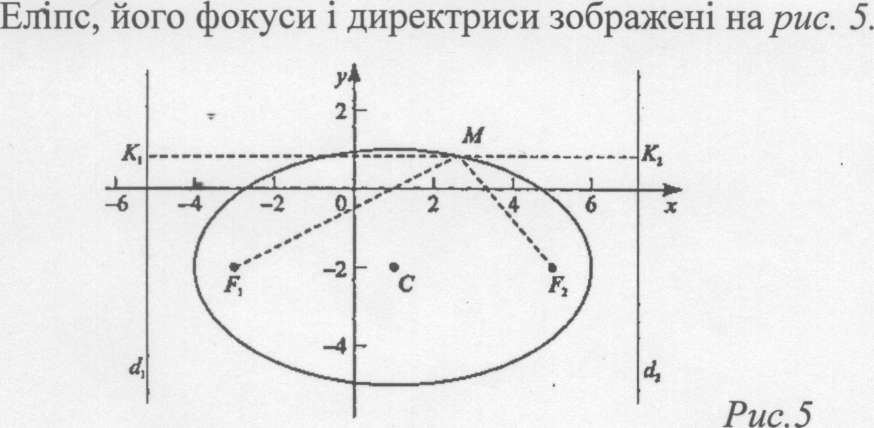
Приклад. Побудувати еліпс, заданий рівнянням 9х² - 18х + 25у² + ЮОу -116 = 0.

Знайти ексцентриситет, координати фокусів і рівняння директрис . Побудувати фокуси та директриси.

Розв'язання. Виділимо повні квадрати:

9(х² - 2х +1) - 9 + 25 (у + 4у + 4) -100 -116 = 0.

Звідси : ^ + ⁺ ^ = і.

25 9 ■

З рівняння "(З,) робимо висновок, що це еліпс з центром у точці С(1;-2) і

півосями а= 5,Ь = 3. Фокуси віддалені від центра на відстань с = ліа² -Ь² =4і лежать на великій осі. Тому Рі (~2>\ -2); (5; -2);

с 4

Ексцентриситет є = —=—=0,8 .Директриси сії і сі₂

а 5

сі 5 23 *

віддалені від центра на відстань — = — = — = 6,25 . Тому їх

рівняння х = 1 ± 6,25, х = 7,25 або л; = -5,25.

з прямою і⁷/^, а вісь Оу проходила через середину РіР₂ (рис. 6) .Тоді Т⁷/ (~с;0); Р₂(с;0); М(х,у); ^(х + с)² + у² , Р₂М = ^_х-_с)²+у² .

За означенням гіперболи

| ^(х + сУ+у² + _Л/(*-с)²+/ | =2а.

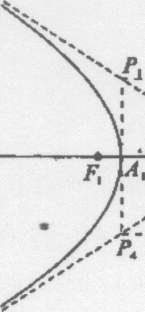
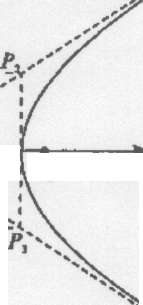
Рис. 6

уі

я.

Після перетворень, що повністю аналогічні перетворенням, які виконувались при виведенні рівняння еліпса, отримаємо

2 2

С -а 2 2 2 2 5—х -у -с -а

а

Позначимо Ь¹ - с = а² (нагадаємо, що для гіперболи с> а). Тоді

и²-

^Ь-х²-у²=ь²

а

• • * 2 Поділивши обидві частини рівняння на Ь , отримаємо канонічне рівняння

(4)

гіперболи

А²

а о

Із цього рівняння безпосередньо випливає, що початок координат є центром симетрії гіперболи, а осі координат — осями симетрії.

Означення. Пряму І називають асимптотою лінії у, якщо при прямуванні довільної точки М лінії у у нескінченність відстань від точки М до прямої І прямує до нуля.

Можна довести, що гіпербола, яка задана рівнянням (4), має

Ь Ь

дві асимптоти, рівняння яких у = — X і у = —х (див. рис. 6).

а а

Пряму Т⁷//^ називають дійсною віссю гіперболи. Точки А!(-а; 0) і А₂ (а; 0) — вершини. Пряма В_}В₂ — уявна вісь гіперболи. Якщо а = Ь, то гіперболу називають рівнобічною.

Означення. Ексцентриситетом гіперболи називають число є = —.

а

Оскільки для гіперболи с > а, то її ексцентриситет перевищує одиницю:

Ь. 2

с

Б = — = а

-,! + (-) а

а

Чим менший ексцентриситет гіперболи, тим сильніше її вітки "стиснуті" до дійсної осі.

Означення. Директрисами гіперболи називають прямі, які перпендикулярні до

її дійсної осі і розміщуються на відстані — від її центра.

Директриси гіперболи не перетинають гіперболу (оскільки є > 1; — < а) (рис. 7).

є

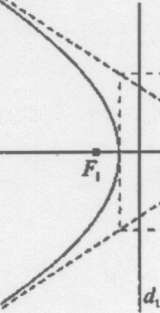
Уп

К,

0

4,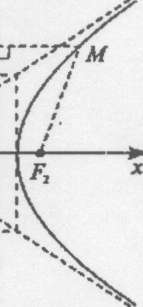

Рис. 7

Для гіперболи, заданої рівнянням (4), директриси мають рівняння х=~— тах= —.

= 1. (3) 4

® 9