3. Инерционное звено первого порядка (апериодическое звено)

При передаче на вход единичного ступенчатого воздействия имеем дифференциальное уравнение следующего вида:

Ty'(t)+y(t)=kx(t)

Перейдем в оперативную форму (через оператор Лапласа):

ПереходTpy(p)+y(p)=kx(p)

Оператор или передаточная функция

W(p)=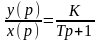

Заменим p=iω

Krx=W(iω)=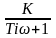

Домножим на сопряженное число числитель и знаменатель.

W(iω)=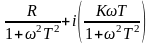

W(i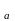 )=Rω+iI(ω)

После преобразования Krx можно определить Аrx и φrK

A(ω)= =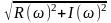

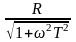
φrx:φ(ω)= =-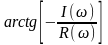

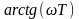
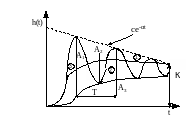
Переходная характеристика будет равна

h(t)=K(1-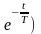

h (t) I

K

t

К – коэффициент передачи

Т – постоянная времени

В частотной области:

iI() K

0 R()

n 1

A()

Arx

1 2 

)

0 

rx

- /2

В качестве примера в электротехнике можно привести R-C цепочки:

R

C

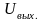
Для гидравлики примером может быть уровень воды в баке с подпором воды на стоке.

Вход – приток; выход – уровень.

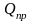
h

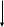
4. Инерционное звено 2-го порядка

Дифференциальное уравнение определяется как:

T y"(t)+T y'(t)+y(t)=K (t)

Перейдем к передаточной функции:

T p y(p)+T py(p)+y(p)=K (p)

W(p)=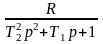

Знаменатель данного выражения является характеристическим уравнением исходного дифференциального уравнения.

Определим корни этого характеристического уравнения.

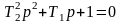
p =-

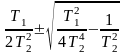
Проанализируем корни данного характеристического уравнения. В результате анализа можно выделить 3 наиболее характерных случая:

1) Т₁ / Т₂ > 2 оба корня вещественные

р₁ = - α_1; р₂ = - α₂

Для первого случая будем иметь решение исходного диф.уравнения в следующем виде:

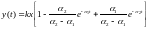
2) р₁ = р₂ = - α =

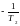
Решение будет иметь вид:

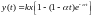
3) Т₁ / Т₂ < 2

,

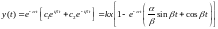
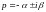
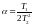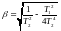
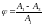- степень затухания процесса

Т – отображает влияние коэф-тов диф. и называется постоянной времени затухания колебания.

Изменяя коэф-ты диф.уравнения можно изменить и характер переходного процесса.