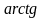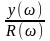Лекция № 4.
При переходе от
дифференциальных уравнений (моделей)
к алгебраической форме представления,
то есть от оригинала к изображению
необходимо для получения k-ой
производной от оригинала достаточно
умножить изображение оригинала на
.
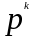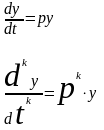
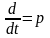
символ дифференцирования
Таким образом, предыдущее Д.У можно представить в виде отношения:
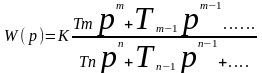
Данное соотношение называется оператором системы или передаточной функцией.
W(p) - передаточная функция
В передаточной функции * мы имеем вход системы – числитель; выход – знаменатель.
Тогда имея модель
Исходя из этого выражения * можно определить порядок решения задач:
Принять x(p);
Определить передаточную функцию W(p) из ДУ;
Определить Y (p);
по таблице соответствий между оригиналом и изображением или же по формуле обратного преобразователя Лапласа определим оригинал Y(t)
Обычно Y(p)=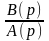
Если числитель и знаменатель, сложные выражения производят разложения на простые дроби, а до нее пользуются таблицей соответствия, таким образом, получена операторная запись модели, называемая передаточной функцией.
Метод переходных характеристик:
Переходная характеристика – это модель системы, представленная во временной области, то есть аргументом является время.
Составим ДУ для различных объектов управлении может быть связано его сложностью и неизученностью протекающих физических, химических и других процессов объекте. Поэтому очень часто используется математическое описание по данным экспериментальных исследований. Суть данного подхода состоит в том, что на вход объекта или системы подается заранее известное по величине и форме воздействие (типовое воздействие).
Тогда реакция или отклик системы на выходе будет отображать динамические свойства системы, иначе говоря, математическая модель.
Данные модели называется динамическими характеристиками.
В динамических характеристиках наиболее часто используется импульсные и переходные характеристики. Представим, что на вход системы подано воздействие:
Для анализа и дальнейшего преобразования этого воздействия в системе, разобьем воздействие некоторое число прямоугольных импульсов.
Разделяя характеристику на последовательность импульсов можно определить реакцию системы на данную последовательность, потому, что следуя один за другим накладываются друг на друга (принцип суперпозиции).
Тогда реакция (отклик) системы на сумму возмущений воздействий импульсов будет равна сумме ее реакций на се импульсы.
Из математики известно:
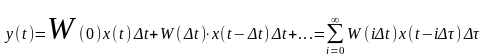
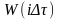-реакция
системы на прямоугольный импульс
Импульс
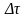представляется единичной площадью с
длительностью
.
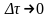Тогда получаем
точное выражение y(t).
В этом точном выражении последовательность
импульсов, площадью
,
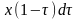а характеристика
будет переходить в W(t):
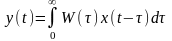- точное выражение
реакции системы на любое входное
воздействие.
Операция над
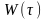и
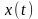называется сверткой функции, а сам
интеграл называется интегралом свертки.
С помощью этого интеграла можно найти реакцию системы на любое воздействие входа , если известна импульсная характеристика .
Однако, экспериментально получить точный график импульсной характеристики невозможно, так как чистом виде невозможно реализовать импульсное воздействие. Поэтому практически пользуются динамическими характеристиками, представляющими собой реакцию системы на ступенчатое или воздействие.
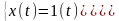при
t>0
и t<0
соответственно
Тогда реакция системы с учетом интеграла свертки будет давать динамическую характеристику, называемую переходной характеристикой h(t).
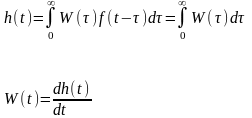
Иначе говоря переходная характеристика представляет собой интеграл от импульсной характеристики, а импульсная характеристика – это производная от переходной.
Переходная характеристика сравнительно несложно получается при воздействии ступенчатого возмущения на выход объекта, в результате чего получаем динамику системы описываемую как переходная характеристика.
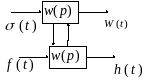
Где W(t) – импульсная и h(t) – переходная характеристики.
Частотные методы описания систем управления.
При использовании частотных методов определяются так же динамические характеристики, но в качестве аргумента этих характеристик выступает не время, а частота.
На вход системы подается последовательность гармонических воздействий. В простейшем случае на вход можно подать периодические воздействия с периодом T.
Мы имеем периодическую функцию, но она может быть разложена в ряд Фурье.
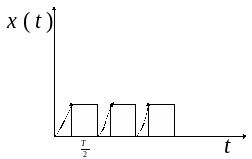
Выберем некоторый интервал T/2. Функция, полученная с помощью разложения в ряд Фурье, называется аппроксимирующей, поэтому ее записывают в виде:
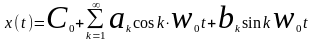
В полярных координатах:
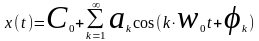где
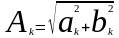- амплитуда k-ой
гармоники.
Лекция №5
При подаче на вход объекта или системы гармонического воздействия на выходе получаем результаты также в виде гармоники или периодической функции, но смещенной по фазе и амплитуде.
Выходную гармонику можно аппроксимировать в виде суммы гармонических воздействий.
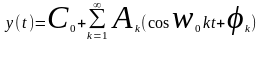
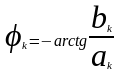
В данном уравнении
не определены только коэффициенты
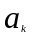
и
,
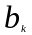а также
.
Согласно Фурье преобразованию они
находятся как :
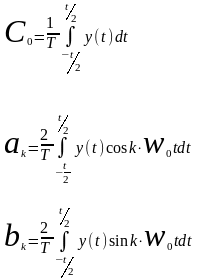
Данные результаты корректны для линейных систем, когда входной бесконечный гармонический сигнал разлагается на сумму гармоник.
Если будет известна реакция системы на каждую из гармоник, то просуммировав данные реакции, мы получим на выходе реакцию на периодическое воздействие x(t).
Но для этого необходимо располагать частотными характеристиками на гармонические колебания разных частот.
Однако нас будут
интересовать частоты кратные
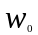
Так как мы приняли в качестве реперных точек кратные частоты, то в предельном переходе от y(t) и действительной y(t) интервал между частотами будет стремиться к 0.
Это означает, что
бесконечный сигнал при T
,
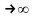а значит при
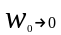интервал между частотами будет стремиться
к 0 и практически будет занимать весь
частотный диапазон.
Частотные характеристики можно найти экспериментально, если подать на вход системы последовательно сигналы различных частот и зафиксировать их реакцию на выходе из системы.
При подаче на вход системы различных частот мы можем получить на выходе динамическую характеристику, определяющую свойства системы.
Для рассмотрения случая можно найти отношение амплитуд:
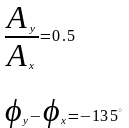
Назовем амплитудно - частотной характеристикой системы зависимость от частоты отношение амплитуд выходных и входных установившихся гармонических колебаний
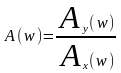(АЧХ)
Определим как фазо - частотную характеристику (ФЧХ)
Сдвиг фаз между входными и выходными гармоническими установившимися колебаниями.
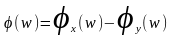
Можно определить,
что
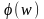практически.
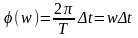
Нетрудно представить, что для одной и той же частоты амплитудные и фазные характеристики (АЧХ и ФЧХ) можно трактовать как вектор, модуль которого является ордината АЧХ и фаза ФЧХ.
Таким образом, мы перешли к понятию комплексно-частотной характеристики.
Если комплексной плоскости используем АЧХ и ФЧХ , получим какой - то вектор.
Комплексно-частотная характеристика – это геометрическое место точек концов 3 векторов, модули которых ординаты АЧХ, а фазы – ординаты ФЧХ.
КЧХ – это характеристика системы, представляющая собой преобразованную по Фурье импульсную характеристику системы.
Между собой временные модули в виде переходных характеристик, дифференциальных уравнений, передаточных функций и частотных характеристик взаимосвязаны.
В качестве примера рассмотрим связь между ДУ и частотными характеристиками:
ДУ
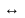ЧХ
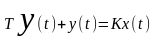
Примем, что в качестве x(t) гармоническая функция.
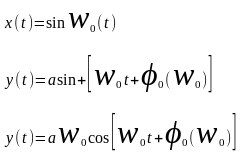подставим в
исходное дифференциальное уравнение.
В результате подстановки и преобразования,
получим:
φ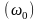
=
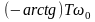
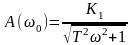общий случай
где
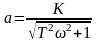частный случай
2)
Связь между частотными характеристиками
или передаточной функции системы. Будем
считать, что на вход системы подан
гармонический сигнал Х(t)=А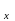
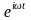
Предположим, что оператор системы
W(p)=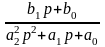
(порядок числителя меньше порядка знаменателя)
Подставим в уравнение периодической функции, преобразованное по Фурье входное воздействие, которое будет иметь
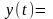
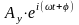
Тогда в результате преобразований мы получим соотношения слудующего вида
W(iω)=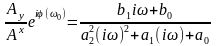
p=iω
Тогда получим Arx, которая связана с передаточной функцией через преобразования Фурье. При этом получается Krx, которая отображается через частоту.
Krx
ω(iω)
Из Krx можно определить модуль и фазу и записать Arx и φrx
Таким образом
W(iω)=K(ω)+i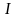
(ω)=A(ω)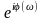
В этой записи
A(ω)=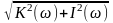
φ(ω)=
-
