3 Алгоритм Саати
Алгоритм основан на сравнении альтернатив, выполняемом одним экспертом. Для каждой пары альтернатив эксперт указывает, в какой степени одна из них предпочтительнее другой.
– Экспертом заполняется матрица парных сравнений размером NxN, где N – количество альтернатив. Матрица заполняется по следующим правилам.
Если i–я альтернатива менее предпочтительна, чем j–я, то указываются обратные оценки (1/3, 1/5, 1/7, 1/9). Могут использоваться промежуточные оценки (2, 4, 6, 8 и 1/2, 1/4, 1/6, 1/8); например, если i–я альтернатива совсем немного лучше j–й, то можно использовать оценку Xij=2 (тогда Xji=1/2). На главной диагонали ставятся единицы.
– Находятся цены альтернатив – средние геометрические строк матрицы:
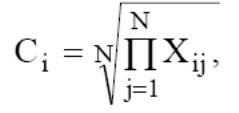2,659;
0,508; 1,225; 0,508
– Находится сумма цен альтернатив:
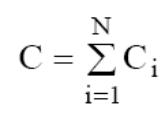В
данном примере C = 2,659 + 0,508 + 1,225 + 0,508=4,9
– Находятся веса альтернатив: Vi = Ci/C.
4 Метод электра
Метод предназначен для решения задач, в которых из имеющегося множества альтернатив требуется выбрать заданное количество лучших альтернатив с учетом их оценок по нескольким критериям, а также важности этих критериев.
Принцип работы метода следующий. Для каждой пары альтернатив (Aj и Ak) выдвигается предположение (гипотеза) о том, что альтернатива Aj лучше, чем Ak. Затем для каждой пары альтернатив находятся два индекса: индекс согласия (величина, подтверждающая предположение о превосходстве Aj над Ak) и индекс несогласия (величина, опровергающая это предположение). На основе анализа этих индексов выбирается одна или несколько лучших альтернатив ("ядро" альтернатив).
1. Переход к безразмерному виду
2. Определяются индексы согласия Cjk,
j=1,...,N, k=1,...,N, N – количество альтернатив.
где Vi – веса критериев;
K+ – подмножество критериев, по которым j–я альтернатива не хуже k–й.
3. Определяются индексы несогласия Djk, j=1,...,N, k=1,...,N.
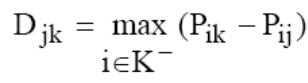
где Pik, Pij – безразмерные оценки;
K– – подмножество критериев, по которым j–я альтернатива не превосходит k–ю.
4. Находится предельное значение индекса согласия:
j=1,...,N
5. Находится предельное значение индекса несогласия:
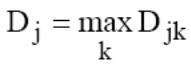j=1,...,N
6. Выделяются лучшие альтернативы («ядро» альтернатив):
Сj > C*, Dj < D*
C*, D* – пороговые значения индексов согласия и несогласия (С*=0,5, D*=0,5).
40. Экспертные системы
Экспертная система (ЭС) – технология извлечения решения из базы знаний, представленной в удобной для машины форме обработки.
Компоненты ЭС: 1) база знаний; 2) машина вывода.
Структура ЭС: Интерфейс пользователя; Пользователь; Интеллектуальный редактор базы знаний; Эксперт; Инженер по знаниям; Рабочая (оперативная) память; База знаний; Решатель (механизм вывода); Подсистема объяснений.
1-ая идея была у Лейбница в 17 веке. Он поставил задачу: «Универсальный решатель задач».
Сложность: 1) язык описания задач; 2) универсальный решатель.
Своеобразной точкой отсчета для работ по созданию экспертных систем можно считать 1965 г., когда ученые из Стэнфордского научно-исследовательского института Эдвард Фейгенбаум и Брюс Бучанан вместе с нобелевским лауреатом Джошуа Ледербергом приступили к созданию компьютерной системы, предназначенной для определения молекулярной структуры химических соединений.
При построении этой системы (Dendral) они в первую очередь создали программу, основанную на системе Аристотелевой логики. С ее помощью формулировалась серия вопросов типа «если - то», которые описывали правила атомных связей. Когда основа системы была готова, ее наполнили сведениями о химических соединениях и способах мышления, которые приводят биохимиков к правильным выводам. Эти сведения были получены путем опроса биохимиков, рассказавших, как они обдумывают те или иные проблемы.
Характеристики ИЗ: не полностью определённые задачи; задачи в которых отсутствует критерии оптимальности; которые не имеют хорошего алгоритма решения; задачи имеют значительное пространство поиска.
Особенностью решения ИЗ является использование «слабых методов»:1) ограниченный и направляемый перебор 2) исключение и отсечение 3) эвристика 4) индукция.
ЭС=БЗ + машина вывода + человек-решатель.