35. Задача линейного программирования

Линейное программирование – математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах  -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Основной (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида:

при условиях

,

.

Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений:

,

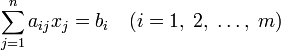Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты   с обратным знаком.

36. Поиск кратчайших путей

Алгоритм Дейкстры (Dijkstra’salgorithm) – алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.

Алгоритм Флойда – Уоршелла – динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом, хотя в 1959 году Бернард Рой (Bernard Roy) опубликовал практически такой же алгоритм, но это осталось незамеченным.

Алгоритм Беллмана–Форда — алгоритм поиска кратчайшего пути во взвешенном графе. За время O(|V| × |E|) алгоритм находит кратчайшие пути от одной вершины графа до всех остальных. В отличие от алгоритма Дейкстры, алгоритм Беллмана–Форда допускает рёбра с отрицательным весом. Предложен независимо Ричардом Беллманом и Лестером Фордом.

37. Принятие решений при многих критериях

Все задачи принятия решений делятся на:

Однокритериальные (на основе 1 критерия); 2) Многокритериальные

По виду решения:

-дискретные(множество решений конечно); - непрерывные

Проблемы при выборе решений при множестве критериев:

Противоречивость критериев 2) невозможность аналитического выражения связей между коэффициентами по разным критериям. 3)оценки по разным критериям могут иметь разный вид (да, нет, хорошо, очень хорошо). 4)численныекритерии отличаются по размерности, направлению и т.п. 5) различие критериев по важности. 6)перечень альтернатив для выбора. 7)перечень критериев по которым следует сравнивать альтернативы. 8)суждения о важности критериев. 9)ограничения по отдельным критериям. 10)парные сравнения альтернатив.

Основные методы: 1) переход от оценок различного вида к оценкам экспертного вида. 2)для числовых оценок используется переход к оценкам, значение которых лежит от 0 до 1 и идут к мах. 3)перевод словесных оценок в числовую форму с использованием шкалы Харингтона, при этом оценка соответствует значениям 0.8-1; 0,63-08; 0,37-0,63; 0,2-0,37; 0-0,2 (эти значения могут меняться).

Классификация процедур принятия решений:

Класс	Пример	Решение задачи
1	Методы на основе лексикографического упорядочивания критерия	Непрерывно дискретные задачи с чётким различием по критериям важности
Методы на основе компенсации критерия	Метод последовательных уступок	Непрерывно дискретная задача с небольшим числом критериев
На основе вычисления обобщённых оценок альтернатив	Метод эффективной стоимости, оценки структур, функции полезности	Дискретные задачи с числовыми критериями
Методы на основе попарных альтернатив	Метод анализа и иерархии, метод Электра	Дискретные задачи с критерием любого вида
Методы на основе выявления суждения ЛПР	Метод-запрос	Дискретные задачи с критерием любого вида