34. Методы минимизации функций нескольких переменных

Из курса математического анализа известны следующие условия минимума функции n переменных.

1. Если в точке х0  En функция f (x) дифференцируема и достига­ет локального минимума, то

f  (х0) = 0 или , j = 1,…, n (1)

(необходимое условие минимумa). Точки, в которых выполнено усло­вие (3.12), называются стaционaрными точкaми дифференцируемой функции f (x).

2. Если в стационарной точке х0  En , функция f (x) дважды дифференцируема и матрица ее вторых производных f  (х0) положительно определена, то х0 есть точка локального минимума f (x) (достаточное условие минимумa).

Классический метод

Шаг 1. Решив систему уравнений (1), найти все стационарные точки функции f (x).

Шаг 2. Используя достаточные условия минимума, среди стационарных точек функции f (x) найти точки локального минимума и, срав­нивая значения функции в них, определить точки глобального минимума.

Минимизация по правильному симплексу

Правильным симплексом в пространстве En называется множество из п + 1 равноудаленных друг от друга точек (вер­шин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса.

В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, в E3 – правильного тетраэдра.

Шаг 0. Выбрать параметр точности , базовую точку х0 , ребро a и построить начальный симплекс по формулам 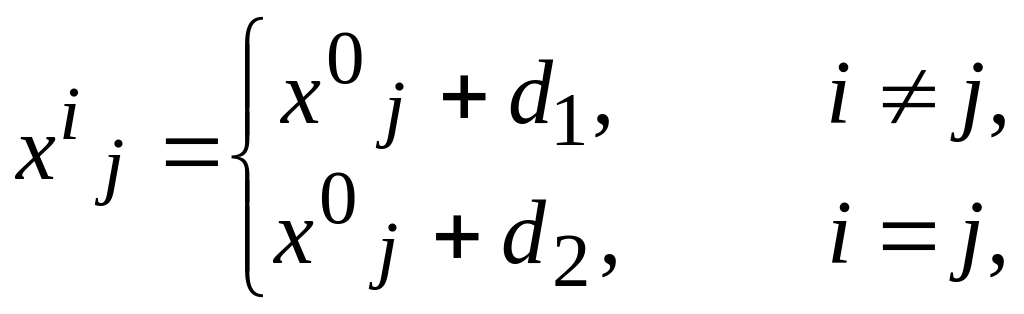где d1 , d2 , a– длина ребра.. Вычислить f (х0).

Шаг 1. Вычислить значения f (х) в вершинах симплекса х1 , .., xn .

Шаг 2. Упорядочить вершины симплекса х0 , .., хn так, что бы f (х0)  … f (х1)  f (хn–1)  f (хn).

Шаг 3. Проверить условие

(3.38)

Если оно выполнено, то вычисления прекратить, полагая х*  х0 , f *  f (x0).

В противном случае перейти к шагу 4.

Шаг 4. Найти и выполнить отражение вершины хn:

=2xc – хn .Если f ( ) <f (xn), то положить хn= и перейти к шагу 2. Иначе – перейти к шагу 5.

Шаг 5. Найти и выполнить отражение вершины хn–1: = 2x c – хn–1. Если f ( ) < f (хn–1), то положить хn–1 = и перейти к шагу 2. Иначе – перейти к шагу 6.

Шаг 6. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной х0 . Остальные п вершин симплекса найти по формуле хi = (хi + х0)/2, i=1, .., п. Перейти к шагу 1.

Геометрическая иллюстрация работы алгоритма в пространстве показана на рис., где точки х0 , х1 , х2 – вершины начального симплекса, а пунктиром указаны процедуры отражения.

Метод циклического покоординатного спуска

Этот метод заключается в последовательной минимизации целе­вой функции f (x) сначала по направлению первого базисного вектора е1, затем второго – е2 и т.д. После окончания минимизации по направ­лению последнего базисного вектора еn цикл повторяется.

Шаг 0. Выбрать х  En , критерий достижения точности (напри­мер, (хk+1, хk) < 1 ;  или f (xk+1)–f (xk) < 2) ;величину . Найти f (x), положить j= 1.

Шаг 1. Решить задачу одномерной минимизации Ф() = f (х + еj) min,   R, т.е. найти *. Положить = х +*еj, вычис­лить f (х).

Шаг 2. Если j < п, то положить х = , j=j+1 и перейти к шагу 1, иначе – перейти к шагу 3.

Шаг 3. Проверить условие достижения точности ||х– || <  или | f (x) – f ( )| <. Если оно выполняется, то положить х* = , f  *=f ( ) и закончить поиск. Иначе – положить х = , f (х) = f ( ), j = 1 и перейти к шагу 1.

Методы случайного поиска

Алгоритм 1 (с возврaтом при неудaчном шaге).

Шаг 0. Выбрать параметр точности  > 0, начальный шаг  >0, коэффициент уменьшения шага  >1, предельное число неудачных попыток N, начальную точку х. Вычислить f (х).

Шаг 1. Положить счетчик числа неудачных попыток j= 1.

Шаг 2. Получить реализацию случайного вектора .

Шаг 3. Найти пробную точку y=x+/||||, вычислить f (у).

Шаг 4. Если f (у)< f (х), то положить х = у, f (х) = f (у) и перейти к шагу 3. Иначе – перейти к шагу 5.

Шаг 5. Положить j =j + 1. Если j < N, то перейти к шагу 2, иначе к шагу .

Шаг 6. Проверка условия достижения точности. Если  < , то поиск завершить, полагая х*=х, f  *= f (х). Иначе – положить  = /у и перейти к шагу 1.

Иллюстрация построения последовательности (3.41) с помощью описанного алгоритма для функции двух переменных приведена на рис. 3.10, где пунктиром показаны неудачные попытки определения хk+1 из (3.41), не приводящие к уменьшению f (х).

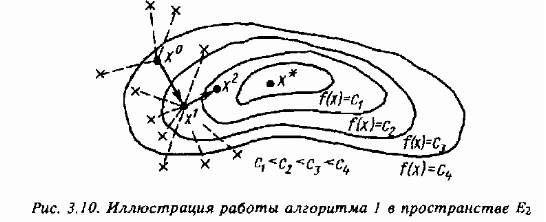
Рис. 3.10. Иллюстрация работы алгоритма 1 в пространстве Е2.

Замечание. На практике предельное число неудачных попыток N обычно полагают равным 3п, где п – число переменных целевой функции.

Алгоритм 2 (наилучшей пробы).

Этот алгоритм отличается от предыдущего только шагами 2 и 3:

Шаг 2. Получить т реализации случайного вектора : 1 , …, m

Шаг 3. Найти пробные точки yi = , i = 1,.., т, вы­делить f (уi). Найти уk из условия f (уk)= и положить у= уk .

Методы безусловной минимизации, использующие производные функции

Пусть функция f (x) дифференцируема в En . В этом разделе рас­сматриваются итерационные процедуры минимизации вида

X k = x k–1 + k p k, k =1, .., x0  En, (3.48)

где направление убывания рk определяется тем или иным способом с учетом информации о частных производных функции f (x), а величина шага а^>0 такова, что

f (x k) < f (x k–1), k =1,2,.. (3.49)

Так как функция предполагается дифференцируемой, то в ка­честве критерия останова в случае бесконечной итерационной по­следовательности {хk}, как правило, выбирается условие (3.30): ||f  '(xk )|| <, хотя, разумеется, могут быть использованы и другие критерии.

Метод градиентного спуска

Шаг 0. Задать параметр точности  > 0, начальный шаг  > 0, подобрать х  En. Вычислить f (х).

Шаг 1. Найти f '(x) и проверить условие достижения точности:

||f  '(x)|| < . Если оно выполнено, вычисления завершить, полагая х* = х, f *=f (х). Иначе – перейти к шагу 2.

Шаг 2. Найти y=x–f  '(x) и f (у). Если f (у) < f (х), то положить x =у, f (х) = f (у) и перейти к шагу 1, иначе – перейти к шагу 3.

Шаг 3. Положить =/2 и перейти к шагу 2.

Метод ньютона

Пусть функция f (x) дважды дифференцируема в En . Тогда для нее можно записать разложение по формуле Тейлора в окрестности точки xk :

f (x) = f  (хk) + < f  '(хk), x–xk > + < f  (хk)(x–xk), x–xk > + ( || x–xk ||2 )

Отсюда видно, что поведение функции f (x) с точностью до величины порядка ( || x–xk ||2 ) может быть описано квадратичной функцией

Фk(x) = < f  (хk)(x–xk), x–xk > + < f  '(хk), x–xk > + f  (хk). (3.68)

Минимизируем функцию Фk(x) вместо f (x). Найдем ее точку минимума xk+1 из условия Фk(x) = 0:

Фk(x) = f  (хk)(x–xk) + f  (хk) = 0. (3.69)

Пусть матрица Гессе f  (хk) положительно определена при всех xEn и, следовательно, невырождена (det f  (хk) > 0). Тогда существует обратная матрица [f (хk)]–1. Отметим, что квадратичная функция (3.68) с положительно определенной матрицей f  (хk) сильно выпукла и уравнение (3.69) определяет единственную точку глобального минимума функции Фk(x). Умножим слева обе части равенства (3.69) на матрицу [f (хk)]–1 и найдем точку минимума xk+1 квадратичной функции (3.68), аппроксимирующей f (x) в окрестности точки

x=xk :

xk+1 = xk – [f (хk)]–1 f  (хk) , k = 0, 1, … (3.70)

Итерационный процесс –, начатый из произвольной точки x0En, называется методом Ньютона минимизации функции многих переменных.