10) Нормальный закон распределения погрешностей

Этот закон применяется при следующих предположениях:

– погрешность D должна принимать непрерывный ряд значений или монотонный в интервале ± ¥;

– при выполнении значительного числа измерений большие погрешности D появляются реже, чем малые, а частота появления погрешностей, равных по абсолютной величине и противоположных по знаку, одинакова.

Для нормального закона распределения

.где s – среднеквадратическое отклонение (СКО) погрешности D, характеризующее точность выполненных измерений (чем меньше s, тем выше точность). По мере уменьшения s рассеяние случайных погрешностей D относительно центра их распределения (в данном случае относительно значения D = 0) уменьшается. На рис. 1.12 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратичного отклонения. Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

Р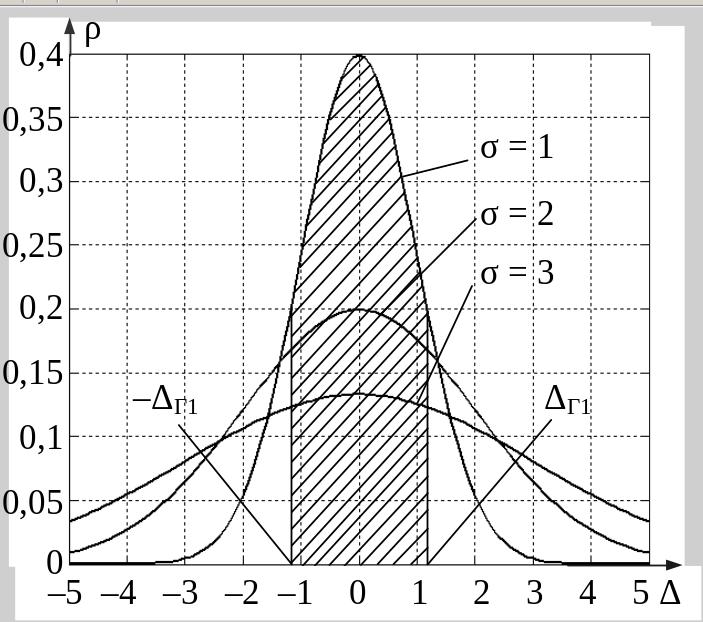 ис. 1.12. Графики нормального закона распределения

плотности вероятности случайных погрешностей

В теории вероятности часто используется такой параметр, как дисперсия D, характеризующая рассеяние погрешности относительно центра распределения. Причем среднеквадратическое отклонение и дисперсия связаны известной в математической статистике формулой .

На графике плотности вероятности для конкретного СКО (см. рис. 1.12) вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией r(D), отрезком оси D от –D_Г1 до D_Г1 и ординатами r(–D_Г1), r(D_Г1). Чем шире заданный интервал погрешностей, тем больше площадь S, т.е. больше вероятность попадания случайных погрешностей измерений D в этот интервал. Для интервала (–¥,+¥) вероятность R(–¥ £ D £ +¥) = 1.

Равномерный закон распределения плотности вероятности

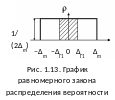
Данный закон применяется тогда, когда случайная погрешность измерений с равной плотностью вероятности принимает любые значения в ограниченном интервале. Этот закон характерен для случайных погрешностей при измерении непрерывных физических величин методом дискретного счета при преобразовании величин в аналого-цифровых преобразователях с поразрядным взвешиванием, из-за погрешности дискретности и квантования, а также для погрешностей отсчета показаний со шкал аналоговых приборов.

Все возможные случайные погрешности результата измерений, описываемых равномерным законом, расположены в интервале (–D_m, D_m), где D_m – максимальная погрешность. Аналитически плотность вероятности ρ(Δ) равномерного закона распределения определяется по формуле:

Вероятность того, что случайная погрешность результатов измерений находится в некотором симметричном интервале (–D_Г1, D_Г1), определяется приведенным выше выражением при подстановке в него значения плотности распределения вероятности ρ(Δ) = 1/2 Δ_m. График равномерного закона распределения плотности вероятности приведен на рис. 1.13.

На графике (см. рис. 1.13) площадь заштрихованного прямоугольника основанием 2D_Г1 и высотой 1/2D_m численно равна вероятности:

.

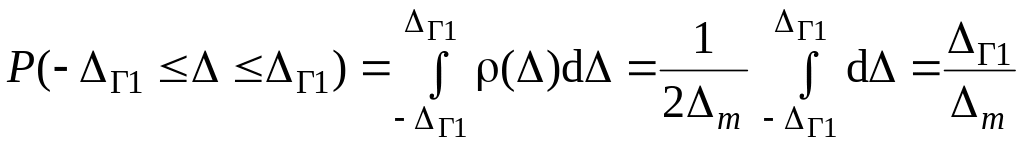Д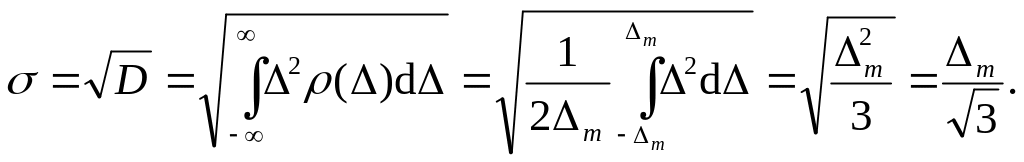 ля равномерного закона, симметричного относительно центра D = 0, расчет случайной погрешности s выполняется с помощью известного из теории вероятностей выражения для дисперсии случайной величины:

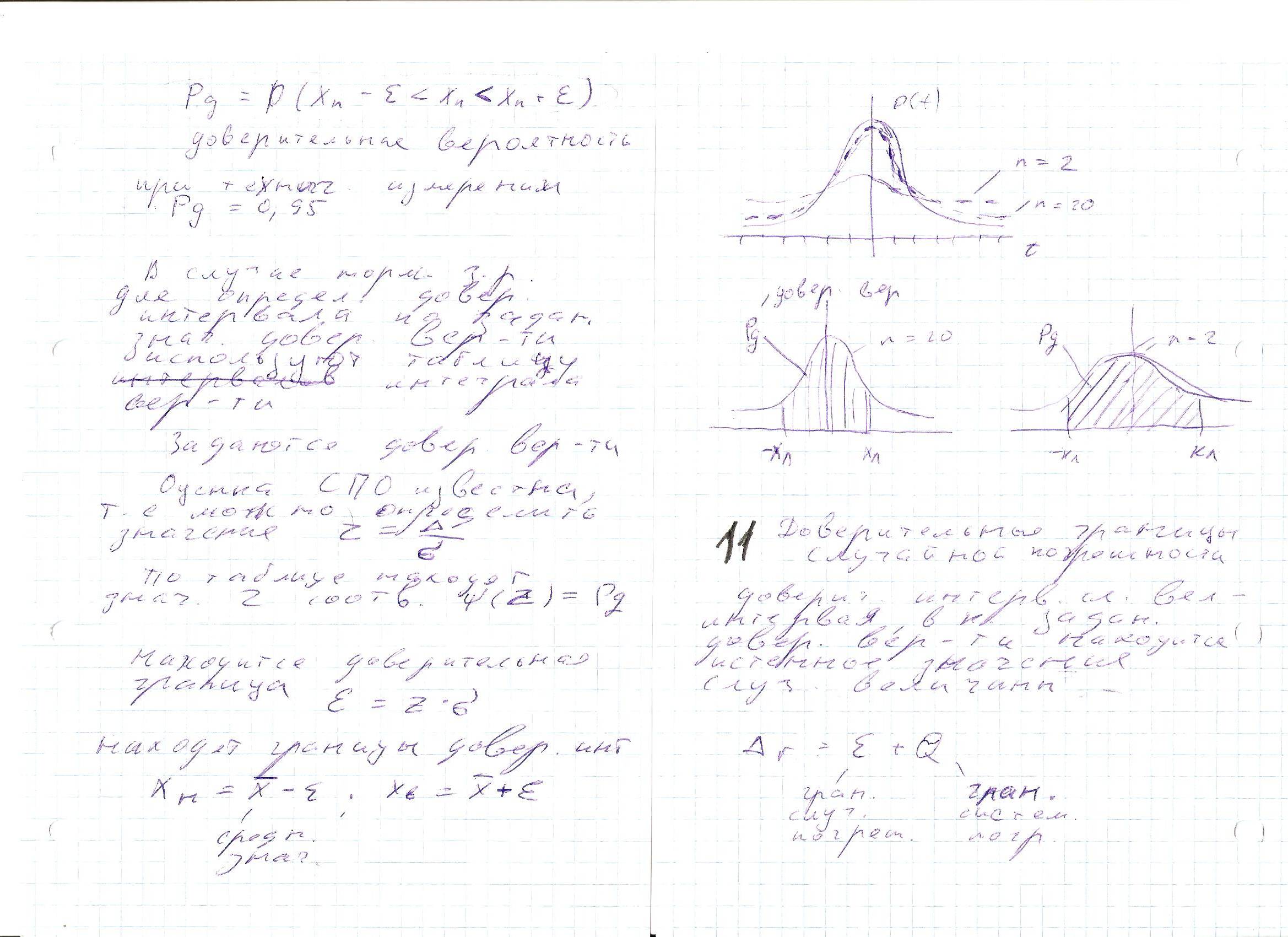1 1)

1 2)