Дисперсия и её свойство

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий: 1. Простая дисперсия  (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

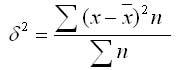
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

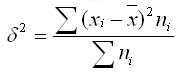Свойства дисперсии.1.Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Внутригрупповая и межгрупповая дисперсия

Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия s2 измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Межгрупповая дисперсия (s2x) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Внутригрупповая дисперсия (s2i) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия. Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

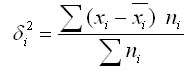где хi — групповая средняя;  ni — число единиц в группе. Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию). Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

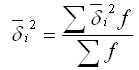Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.