Мода и медиана, их определение в вариационных рядах

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда. В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле: 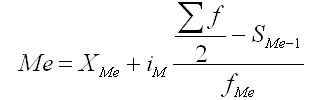где Х_m — нижняя граница медианного интервала; i_m — медианный интервал; S_me— сумма наблюдений, которая была накоплена до начала медианного интервала; f_me — число наблюдений в медианном интервале. Свойства медианы. Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее. Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения. Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины Графическое определение медианы. Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив пополам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы. Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда. Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле: где ХМо — нижняя граница модального интервала; imo — модальный интервал; fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д. Соотношения между средней арифметической, медианой и модой. Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают. К. Пирсон на основе выравнивания различных типов кривых определил, что для умеренно асимметричных распределений справедливы такие приближенные соотношения между средней арифметической, медианой и модой: