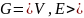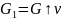28.Теорема Поста. Замкнутые классы функций. Примеры.

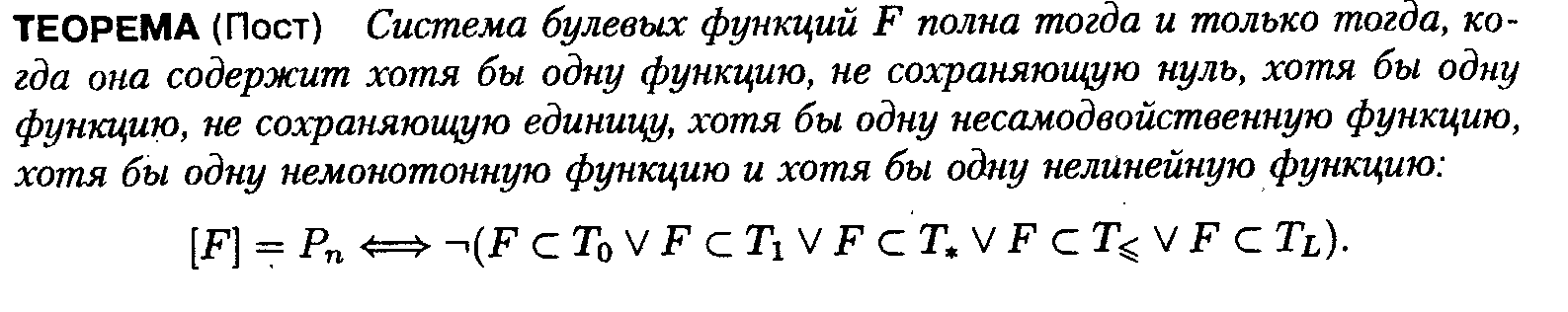
Замкнутый класс в теории булевых функций — такое множество   функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим:  . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества  , снова входит в это же множество.

• Класс конъюнкций K, являющийся замыканием множеств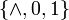а  . Он представляет собой множество функций вида  .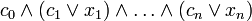

• Класс дизъюнкций D, являющийся замыканием множеств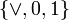а  . Он представляет собой множество функций вида  .

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали:

1. Хотя бы одна функция, не сохраняющая 0.

2. Хотя бы одна функция, не сохраняющая 1.

3. Хотя бы одна нелинейная функция.

4. Хотя бы одна немонотонная функция.

5. Хотя бы одна несамодвойственная функция.

Этому требованию отвечает система функций  . На её основе и строятся полиномы Жегалкина.

29.Определения теории графов. Смежность. Связность. Виды графов(ор-, псевдо- и т.д.).

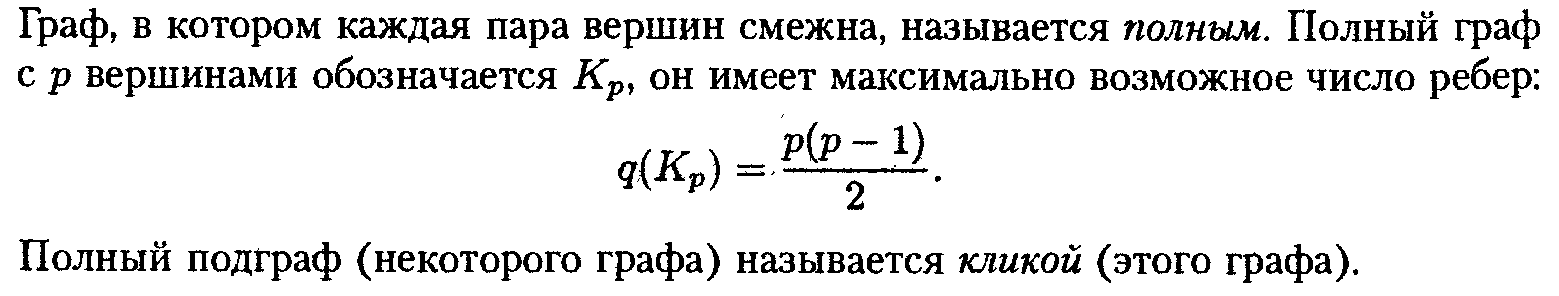
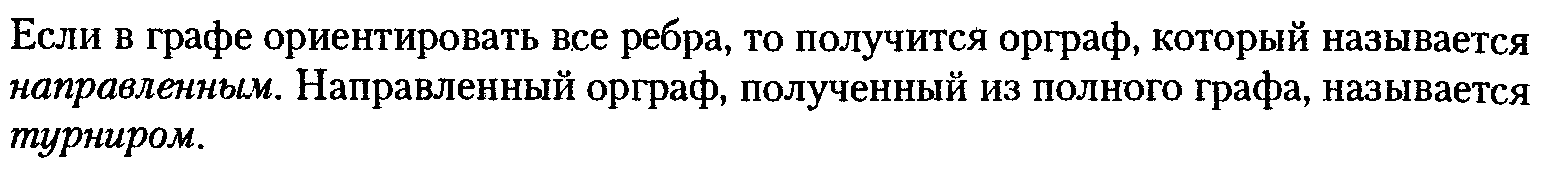
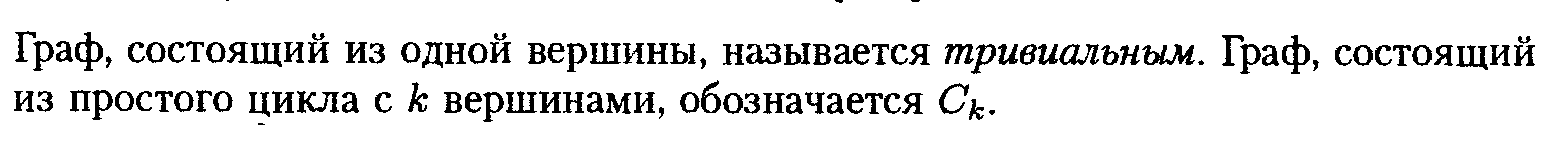
30. Изоморфизм графов. Примеры

31.Элементы графов. Подграфы. Полные подграфы. Клика

32.Маршруты, цепи, циклы. Виды. Связность. Диаметр графа.

Маршрут – чередующаяся последовательности из вершин и ребер, каждые 2 соседних элемента связаны инцидентно.

Если все ребра различны, то маршрут называется цепью. Если все вершины различны, то маршрут называется простой цепью. Если цепь замкнута, то ее называют циклом.

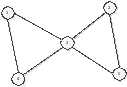
1. 1,3,1,4 маршрут

2. 1,3,5,2,3,4 цепь

3. 1,4,3,2,5 простая цепь

4. 1,3,5,2,3,4,1 цикл

5. 1,3,4,1 простой цикл

Связность

Говорят, что две вершины связаны, если существует соединяющая их цепь. Граф, в котором все вершины связаны называется связным графом. Отношение того, что две вершены связаны – отношение эквивалентности на графе.

Класс эквивалентности по отношению связности двух вершин называется компонентой связности графа.

Число компонентов связности K(G)

Если K == 1 => граф связный. Если K == 2 => граф не связный.

Длина маршрута равна количеству ребер.

Диаметр графа — это максимум расстояния между вершинами для всех пар вершин. Расстояние между вершинами — наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую.

33. Виды графов. Двудольные графы. Операции над графами

Виды графов:

• связным, если для любых вершин u, v есть путь из u в v.

• сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

• деревом, если он связный и не содержит простых циклов.

• полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

• двудольным.

• k-дольным, если его вершины можно разбить на k непересекающихся подмножества V1, V2 , …, Vk так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

• полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

• планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

• взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Двудольный граф – граф у которого множество вершин разбиты на две непересекающиеся части.

Причем каждое ребро этого графа лежит одной вершиной в V1, а второй в V2.

Полный двудольный граф Km,n (задача о колодцах).

Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Орграф в котором есть V1: d⁺(V1) = 0 и V2: d^-(V2) = 0. V1 называют стоком, V2 – истоком.

Операции над графами

1. Дополнение графа

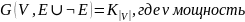
2. Объединение графов

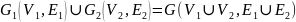
3. Соединение графов

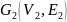
4. Добавление вершины

\

5. Удаление ребра

6. Удаление вершины

7. Стягивание подграфа A в G1(V1, E1)

8. Размножение вершины V