
- •23.Основные булевы функции двух переменных.
- •24.Нормальные формы. Сднф. Скнф.
- •25.Алгоритм построения сднф.
- •26.Полнота системы булевых функций. Примеры полных систем.
- •27 Полином Жегалкина. Полная система для его построения
- •28.Теорема Поста. Замкнутые классы функций. Примеры.
- •33. Виды графов. Двудольные графы. Операции над графами
- •34. Способы представления графов в компьютере
- •35 Орграфы и бинарные отношения. Транзитивные зависимости
- •36 Свободные деревья. Лес. Основные свойства деревьев
- •37 Упорядоченные и бинарные деревья
- •38.Представление деревьев в компьютере.
- •40.ДеревоСортировки.АссоциативныйМассив.Сравнение производительности
- •41.АлгоритмыВставки,удаленияИПоискавДеревеСортировки Поиск элемента (find)
- •Добавление элемента (insert)
- •Удаление узла (remove)
- •Обход дерева (traverse)
- •42.АвЛдеревья.Балансировка
- •43.КратчайшийОстов.АлгоритмКрускала
- •44.КратчайшийОстов.АлгоритмПрима
- •45.ЗадачаНахожденияКратчайшегоПутиНаГрафе.АлгоритмБеллманаФорда
- •Граф с отрицательными циклами
- •46.Алгори́тм Де́йкстры
- •47.АлгоритмА-star
- •51. Алгоритм Форда-Фалкерсона.
- •52. Алгоритм проталкивания предпотока
- •53. Эйлеров цикл. Алгоритм построения.
- •54. Гамильтонов цикл. Задача коммивояжера.
- •55. Раскраска графов. Хроматическое число. Алгоритм раскрашивания
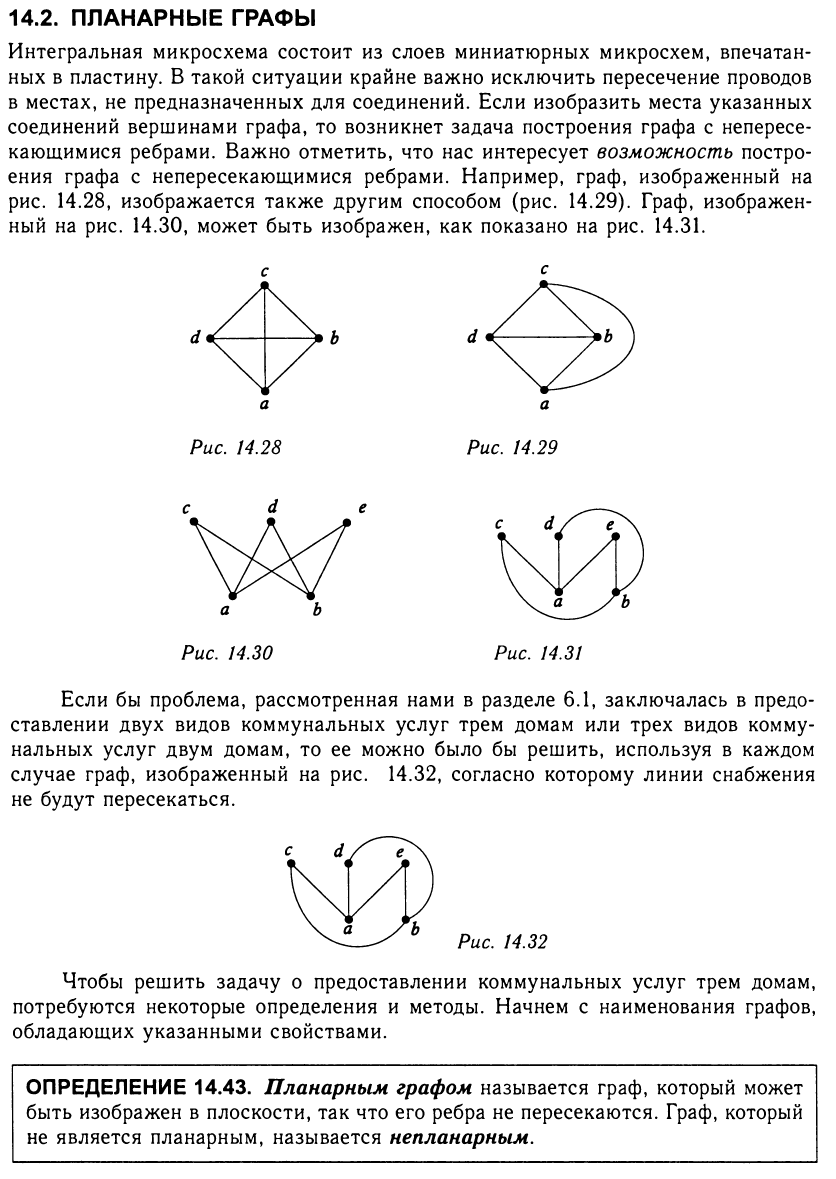
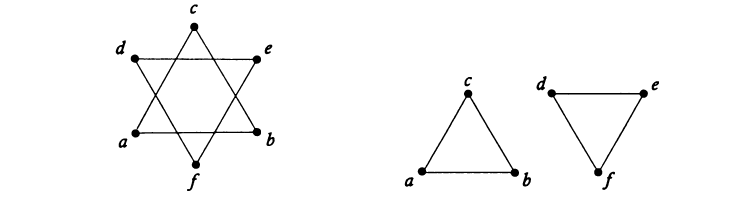
- •56. Планарные графы. Задача укладки графа на поверхность. Примеры планарных графов.
- •Укладка на поверхности
- •57.Теорема о раскарске планарных графов
55. Раскраска графов. Хроматическое число. Алгоритм раскрашивания
56. Планарные графы. Задача укладки графа на поверхность. Примеры планарных графов.

Укладка на поверхности
Пусть σ — произвольная поверхность в трехмерном пространстве.
Граф G, изображенный на поверхности σ, называется уложенным на σ, если его ребра не пересекаются в точках, отличных от вершин.
Граф G укладывается на поверхности σ, если он изоморфен некоторому графу, уложенному на σ.
Свойство графа укладываться на поверхности безусловно зависит от вида этой поверхности. Однако многие поверхности с точки зрения укладки графов ничем не отличаются от плоскости. Принципиально важен следующий случай.
Теорема об укладке графа на сфере
Граф укладывается на сфере тогда и только тогда, когда он планарен.
Укладка графа на торе
После доказательства теоремы об укладке графа на сфере возникает естественный вопрос: существуют ли вообще поверхности, укладка на которых не равносильна планарности? Ответ — да, существуют. Примером такой поверхности является трехмерный тор, который часто называют
«бубликом» (см. рис. 5). За счет наличия «дырки» такой бублик обладает дополнительными возможностями по размещению ребер. На рис. 5 показано, как на торе уложить двудольный граф K3,3, возникающий в задаче о домах и колодцах (невидимые линии проведены пунктиром).
57.Теорема о раскарске планарных графов
Лемма 1. Для любой геометрической реализации на плоскости связного планарного графа с q рёбрами выполняется равенство:

где суммирование ведётся по всем граням (включая внешнюю).
Следствие. В любом связном планарном графе G = (V, E) без петель и кратных рёбер с p ≥ 3 вершинами и q рёбрами справедливо неравенство: q ≤ 3(p – 2).
Определение 1. Подмножество V1 ⊆ V вершин графа G = (V, E) называется независимым, если никакие две вершины из V1 не соединяются ребром.
Определение 2. Пусть есть некоторое множество C = {C1, C2, …, Cm} — множество цветов. Тогда раскраской графа G = (V, E) (вершинной) называется любое отображение φ: V → C. Раскраска называется правильной, если для любого цвета вершины этого цвета образуют независимое множество.
Лемма 2. В планарном графе без петель и кратных рёбер существует вершина v:
deg v ≤ 5. 22
Теорема 10. Вершины любого планарного графа можно правильно раскрасить в не более чем 5 цветов.
