1

Электрическая цепь  — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы, в которых могут быть описаны с помощью понятий сила тока и напряжение.

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

Электрический ток — упорядоченное движение свободных электрически заряженных частиц под воздействием электрического поля. Электрическое напряжение между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы электрического поля, совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.

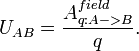
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд. В этом случае электрическое напряжение   между двумя точками совпадает с разностью потенциалов между ними.

Альтернативное определение —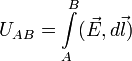 

— интеграл от проекции поля эффективной напряжённости поля   (включающего сторонние поля) на расстояние между точками A и B вдоль заданной траектории, идущей из точки A в точку B. В электростатическом поле значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.

Единицей измерения напряжения в системе СИ является вольт. Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источникахпостоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительногозаряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ). В замкнутом контуре ( ) тогда ЭДС будет равна:

, где   — элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

Рассмотрим вопросы нагревания токоведущих частей электротехнических устройств.

Как известно, согласно закону Джоуля — Ленца при постоянном токе энергия, потребляемая резистивным элементом с сопротивлением r в течение времени t и преобразуемая им в теплоту, определяется по формулам

(1.8)

W = I2rt = UIt =	U2	t = U2gt.
	r

Мощность представляет собой энергию в единицу времени, Р = W/t  Учитывая это, получим следующие выражения мощности:

(1.9)

P = I²r = UI = U²/r = U²g.

Основными единицами электрической энергии и мощности являются соответственно 1 джоуль (1 Дж = 1 В • А • с) и 1 ватт (1 Вт = 1 Дж/с = 1 В • А).

При сравнительно небольших температурах, с которыми работают токоведущие части многих элементов электрических цепей (провода электрических сетей, обмотки электрических машин, аппаратов и др.), можно считать, что количество отдаваемой теплоты пропорционально разности температyp токоведущей части и окружающей среды. В этом случае на основании уравнения теплового равновесия можно получить следующее выражение для установившейся температуры токоведущей части:

(1.10)

t°уст =	I2r	+ t'oкp,
	A

где I²r— количество теплоты, выделяемой за 1с в сопротивлении токоведущей части, равное мощности, потребляемой элементом цепи с сопротивлением r, Дж/с; А — теплоотдача токоведущей части, представляющая собой количество теплоты, отдаваемой в окружающую среду за 1с при разности температур в 1°С, Дж/(с • °С); t°_уст  и t°_окр _  установившаяся температура токоведущей части и температура окружающей среды, °С. Теплоотдача зависит от конструктивных особенностей токоведущей части, ее поверхности и способа охлаждения.

Как видно, установившаяся температура (при данной температуре t°_окр ) зависит от потребляемой резистивным элементом r мощности и теплоотдачи.

Токоведущие части различных элементов электрических цепей должны быть рассчитаны так, чтобы их температура t°_уст не превышала допустимых значений, которые определяются различными факторами. Так, наибольшая допустимая температура изолированных проводов определяется нагревостойкостью изоляции.

Для обоснования применяемой часто методики расчета токоведущих частей по нагреванию предположим, что мы имеем прямолинейный проводник, для которого выражение (1.10) может быть преобразовано к виду

(1.11)

t°уст =	J2ρd	+ t°окр,
	4А0

где А₀— коэффициент теплоотдачи, представляющий собой теплоотдачу с 1м² поверхности охлаждения проводника, Дж/(°С • с • м²); J— плотность тока в проводнике, А/м²; ρ — удельное сопротивление материала проводника. Ом м; d— диаметр проводника, м.

Активная мощность

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: 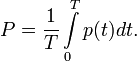  В цепях однофазного синусоидального тока   гдеU и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость gпо формуле   В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 

Исто́чник то́ка (также генератор тока) — двухполюсник, который создаёт ток  , не зависящий от сопротивления нагрузки, к которой он присоединён. В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе кисточнику ЭДС, чем к источнику тока. Идеальный источник тока

Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:

Мощность, отдаваемая источником тока в сеть, равна:

Так как для источника тока  , напряжение и мощность, выделяемая им, неограниченно растут приросте сопротивления.

[Править]Реальный источник тока

Реальный источник тока, так же как и источник ЭДС, в линейном приближении может быть описан таким параметром, как внутреннее сопротивление  . Отличие состоит в том, что чем больше внутреннее сопротивление, тем ближе источник тока к идеальному (источник ЭДС, наоборот, тем ближе к идеальному, чем меньше его внутреннее сопротивление). Реальный источник тока с внутренним сопротивлением   эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление   и ЭДС  .

Напряжение на клеммах реального источника тока равно:

Сила тока в цепи равна:

Мощность, отдаваемая реальным источником тока в сеть, равна:

Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.

В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.

[править]Реальные источники напряжения

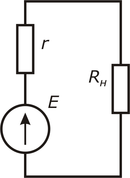
Рисунок 2

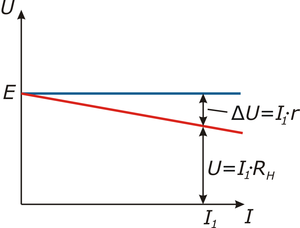
Рисунок 3 — Нагрузочная характеристика

Идеальный источник напряжения (источник ЭДС) является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то ток I, протекающий через него, стремился бы к бесконечности при подключении нагрузки, сопротивление R_H которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как  . Но это невозможно, по той причине, что мощность любого источника энергии конечна.

В реальности, любой источник напряжения обладает внутренним сопротивлением r, которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряжении источника) и наоборот. Наличие внутреннего сопротивления отличает реальный источник напряжения от идеального. Следует отметить, что внутреннее сопротивление — это исключительно конструктивное свойство источника энергии. Эквивалентная схема реального источника напряжения представляет собой последовательное включение источника ЭДС — Е(идеального источника напряжения) и внутреннего сопротивления — r.

На рисунке 3 приведены нагрузочные характеристики идеального источника напряжения (источника ЭДС) (синяя линия) и реального источника напряжения (красная линия).

где

 — падение напряжения на внутреннем сопротивлении;

 — падение напряжения на нагрузке.

При коротком замыкании ( )  , то есть вся мощность источника энергии рассеивается на его внутреннем сопротивлении. В этом случае ток   будет максимальным для данного источника ЭДС. Зная напряжение холостого хода и ток короткого замыкания, можно вычислить внутреннее сопротивление источника напряжения:

Элементом электрической цепи называют идеализированное устройство, отображающее какое-либо из свойств реальной электрической цепи.

Электрические цепи, в которых параметры всех элементов не зависят от величины и направлений токов и напряжений, т.е. графики вольт-амперных характеристик (ВАХ) элементов являются прямыми линиями, называются линейными. Соответственно такие элементы называются линейными.  Когда параметры элементов электрической цепи существенно зависят от тока или напряжения, т.е. графики ВАХ этих элементов имеют криволинейный характер, то такие элементы называют нелинейными.  Если электрическая цепь содержит хотя бы один нелинейный элемент, то она является нелинейной электрической цепью.

В теории электрических цепей различают активные и пассивные элементы. Первые вносят энергию в электрическую цепь, а вторые ее потребляют.

Пассивные элементы электрических цепей

Резистивным сопротивлением называется идеализированный элемент электрической цепи, обладающий свойством необратимого рассеивания энергии.

Активные элементы электрических цепей

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.2) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

2

Пассивные элементы электрических цепей

Резистивным сопротивлением называется идеализированный элемент электрической цепи, обладающий свойством необратимого рассеивания энергии. Графическое изображение этого элемента и его вольт-амперная характеристика показана на рисунке (а - нелинейное сопротивление, б -линейное сопротивление).

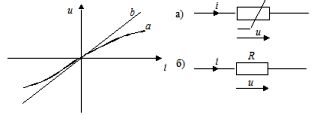
Напряжение и ток на резистивном сопротивлении связаны между собой зависимостями: u = iR, i = Gu. Коэффициенты пропорциональности R и G в этих формулах называются соответственно сопротивлением и проводимостью и измеряются в омах [Ом] и сименсах [См]. R = 1/G.

Индуктивным элементом называется идеализированный элемент электрической цепи, обладающий свойством накопления им энергии магнитного поля. Графическое изображение этого элемента показано на рисунке (а - нелинейного, б - линейного).

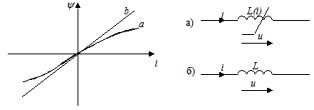
Линейная индуктивность характеризуется линейной зависимостью между потокосцеплением ψ и током i, называемой вебер-амперной характеристикой ψ = Li. Напряжение и ток связаны соотношением u = dψ/dt = L(di/dt)

Коэффициент пропорциональности L в формуле и называется индуктивностью и измеряется в генри (Гн).

Емкостным элементом (емкостью) называется идеализированный элемент электрической цепи, обладающий свойством накапливания энергии электрического поля. Графическое изображение этого элемента показано на рисунке. (а - нелинейного, б - линейного).

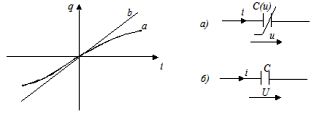
Линейная емкость характеризуется линейной зависимостью между зарядом и напряжением, называемой кулон-вольтовой характеристикой q = Cu

Напряжение и ток емкости связаны соотношениями i = dq/dt =C(du/dt).

3

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока исопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде :  ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС)  , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

•  — ЭДС источника напряжения(В),

•  — сила тока в цепи (А),

•  — сопротивление всех внешних элементов цепи (Ом),

•  — внутреннее сопротивление источника напряжения (Ом).

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

 (3)

(где   есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

 (4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

 (5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

 (6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).