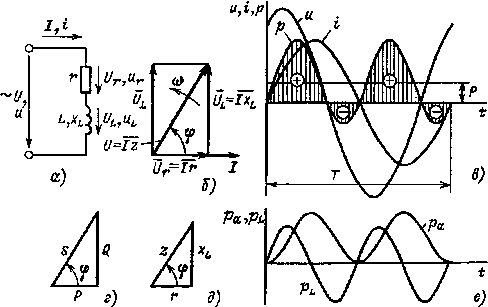Цепь, содержащая катушку с активным сопротивлением r и индуктивностью l

Реальная катушка (обмотка) любого электротехнического устройства обладает определенным активным сопротивлением r и индуктивностью L. Для удобства анализа таких цепей катушку обычно изображают в виде двух идеальных элементов — резистивного r и индуктивного L, соединенных последовательно (рис. 2.9, а). Используя выводы, вытекающие из анализа идеальных цепей, участок цепи с индуктивностью L будем рассматривать как участок, обладающий индуктивным сопротивлением х_L. Уравнение напряжений, составленное по второму закону Кирхгофа для цепи с r и L, имеет вид

u = u_r + u_L.

Выразив напряжения u_r и u_L через ток i = I_m sin ωt и сопротивления участков цепи r и х_L, получим

u = Imr sin ωt + ImxL sin(ωt +	π	),
	2

Рис. 2.9. Электрическая цепь, содержащая катушку индуктивности r и L(а), ее векторная диаграмма (б), графики мгновенных значений u, i, р (в), треугольники мощностей и сопротивлений (г, д), графики мгновенных значений рa , pL (e)

где u_r = I_mr sin ωt — напряжение на активном сопротивлении (активное   напряжение),   совпадающее   по   фазе   с   током;   u_L = I_mx_Lsin (ωt + π/2) — напряжение на индуктивном сопротивлении   (индуктивное   напряжение),   опережающее   ток   по   фазе на 90°.

На векторной диаграмме (рис. 2.9, б) вектор  Ū_r совпадает с вектором тока, а вектор Ū_Lопережает вектор тока на 90°.

Из диаграммы следует, что вектор напряжения сети равен геометрической сумме векторов Ū_r иŪ_L:

Ū = Ū_r + Ū_L,

а его значение

U = √U_r² + U_L².

Выразив напряжения через ток и сопротивления, получим

U = √(I_r)² +(Ix_L)² = I√r² + x_L².

Последнее выражение представляет собой закон Ома цепи r, x_L

I =	U	=	U	,
	√r2 + xL2		z

где z = √r² + x_L² — полное сопротивление цепи, Ом.

Из векторной диаграммы следует, что напряжение цепи r, L опережает по фазе ток на угол φ и его мгновенное значение

u = U_m sin (ωt + φ)

Графики мгновенных значений напряжения в тока цепи изображены на рис. 2.9, в.

Угол сдвига по фазе φ между напряжением и вызванным им током определяют из соотношения

(2.15)

cos φ =	Ur	=	Ir	=	r	=	r	.
	U		Iz		z		√r2 + xL2

Как видно, cos φ и, следовательно, угол φ зависят только от параметров цепи r и x_L.

Разделив стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 2.9, д), Стороны треугольника сопротивлений представляют собой отрезки, а не векторы, так как сопротивления есть постоянные, не изменяющиеся синусоидально величины.

Мгновенная мощность цепи с r и L равна произведению мгновенных значений напряжения и тока:

р = ui = I_m sin ωt U_m sin (ωt + φ).

Средняя мощность за период

	1 T	T		1 Т	T
Рср =		∫	ui dt =		∫	ImUm sin ωt • sin (ωt + φ) dt.
		0			0

Выразив произведение  синусов  через  разность  косинусов, после почленного интегрирования получим

(2.16)

	1 T	T	UmIm 2
Рср =		∫		[cos φ — cos(2ωt + φ)] dt = UI cos φ.
		0

Подставив в (2.16) вместо cos φ его значение из (2.15), получим

(2.17)

Рср = UI cos φ = UI	r	= I2r = P.
	z

Из (2.17) вытекает, что среднее значение мощности в цепи с r и L есть активная мощность, которая выделяется в активном сопротивлении r в виде теплоты.

График  мгновенной   мощности   изображен   на   рис.   2.9, в.

Из графика p_a(t) видно, что активная мощность непрерывно поступает  из сети  и выделяется в  активном  сопротивлении в виде теплоты. Она равна

	1 T	T
Р=		∫	UmrIm sin2 ωt dt = UrI = UI cos φ.
		0

Мгновенная мощность р_L, обусловленная энергией магнитного поля индуктивности, циркулирует между сетью и катушкой. Ее среднее значение за период равно нулю:

	1 T	T		π 2
РL =		∫	UmLIm sin ωt • sin (ωt +		) dt = 0.
		0

Вопрос № 14. Реальный конденсатор