
- •18. Интегральный признак сходимости знакоположительных рядов (Признак сходимости Каши).
- •26.Примеры разложение функций в степенные ряды. Применение степенных рядов в приближенных вычислениях
- •33.Числовые характеристики дискретной случайной величины.
- •34. Биноминальный закон распределения вероятностей случайной величины.
- •36. Плотность распределения вероятностей непрерывной случайной величины. Свойства.
- •3 8. Числовые характеристики непрерывных случайных величин.
1.ДУ
I-го
порядка. Общ. и част. решения. Задача
Коши. Теорема сущ. единственности
решения зада- чи Коши. ДУ
I-го
порядка F(x,y,y’)=0.
Если в данном ур-ний выразить произ-
водную (y’)
то пол- учим ур-ние вида y’=f’(x,y)
к/е наз-ся диф. уравнение разложенным
относительно y’.
ДУ I-го
порядка имеет бесчисленное множество
решении к/е оп-ся форму- лой содержащей
произ- водную постоянную. Опред:
общим решением (общ. интегралом) ДУ I
порядка называется ф-ия y=y(x,C)
к-ая при любом значении «C»
удовлетво- ряет уравнению. Опред:
Частным решением (час. интеграл) наз-ся
решение получаемое из общего при
конкретном значении постоянном «С».
График любого частного реш-ия диф ур-я
наз-ся интеграль- ной кривой. Общему
реш-ию соответсвует семейство интегральных
кривых. y(x0)=y0<=>{ .
Нахождение частного р-ия по заданным
начальным уславиям наз-ся задачей
Коши. Укажем
достаточные условия существования и
единственности решения задачи Коши
.
.
Нахождение частного р-ия по заданным
начальным уславиям наз-ся задачей
Коши. Укажем
достаточные условия существования и
единственности решения задачи Коши
.
![]()
2.ДУ
ур-я с разделяющимися переменными и
приводящиеся к ним.
Рассмотрим диф-е ур-е вида y’=f(ax+by+c)
данное ур-е можно преобразовать к ур-ию
с разделяющимися пере-менными с помощью
замены z=
ax+by+c
где z
неизвестная ф-ия. z’=(
ax+by+c)’=a+by’
выразим y’=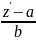 подставляем в исходное ур-е
подставляем в исходное ур-е
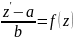 ; z’=f(z)b+a
;
; z’=f(z)b+a
;

 вычисляя
интегралы получим общее решение диф.
ур-я.
вычисляя
интегралы получим общее решение диф.
ур-я.
3.ДУ
I-го
порядка, однородные относительно x
и y,
и приводящиеся к ним.
f(x,y)
– наз-ся однородной ф-ей если при
умножении пере- менных x
и y
на произвольный параметр t
значение ф-ии не изменится. Диф-е ур-е
вида y’=f(x,y)
будет яв-ся однородным если ф-я f(x,
y)
однородная ф-я. Однородное диф ур-е
можно преобразовать к виду y’= (
( ).
Для решения данного ур-я необходимо
сделать замену y=xz,
где z
неизвестная ф-я. y’=x’z+xz’=>
y’=z+xz’
z=
; z+xz’=
).
Для решения данного ур-я необходимо
сделать замену y=xz,
где z
неизвестная ф-я. y’=x’z+xz’=>
y’=z+xz’
z=
; z+xz’=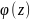 ;
xz’=
-z;
z’=
;
xz’=
-z;
z’=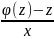 ;
;
 ;
Свели однородное ур-е к ур-ю с раздельными
перемен- ными.
;
Свели однородное ур-е к ур-ю с раздельными
перемен- ными.
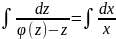 в
рез-те пол-ем общее решение. Диф-е ур-е
вида M(x,y)dx+N(x,y)dy=0
будет однородным если ф-ии M(x,y)
и N(x,y)
– однородные.
в
рез-те пол-ем общее решение. Диф-е ур-е
вида M(x,y)dx+N(x,y)dy=0
будет однородным если ф-ии M(x,y)
и N(x,y)
– однородные.
4.ДУ I-го порядка, линейные относительно неизвестной функции её производной. ДУ I-го порядка наз-ся линейным если оно содержит ф-ю y и её производную y’ в первой степени и не содержит произведений y на y’. Линейное ур-е имеет вид: y’+p(x)y=f(x) Для решения данного ур-я необходимо сделать замену y=u(x)*v(x), где u(x) и v(x) – неизвестные ф-ии y=uv; y’=u’v+uv’; u’v+uv’+p(x)uv=f(x); v(u’+p(x)u)+uv’=f(x). Пусть 1) выражение (u’+p(x)u)=0, тогда 2) uv’=f(x). Таким образом свели лин-е ур-е к 2м ур-ям с разделяющимися переменными решая к-е по порядку (1,2) получим неизвестные ф-ии u и v которые подставляя в y дадут общее решение.
5.метод Бернулли нахождение общего решения ДУ I-го порядка, линейного относительного неизвестной ф-ии и ее производной. Некоторые диф ур-я могут быть приведены к линейным ур-ям с помощью преобразований. К ним относится ур-е Бернулли вида: y’+p(x)*y=f(x)*gn; при n=1 ур-е Бернулли становится ур-ем с разделяющимися переменными; при n=0 приволится к линейному ур-ю. в остальных случаях так же с помощью замены его можно привести к линейному виду, а метод решения такой же как и для линейного ур-я.
6.ДУ
в полных дифференциалах.
Диф ур-е вида P(x,y)dx+
Q(x,y)dy=0
яв-ся ур-ем полных диф-ов если ф-ии P(x,y)
и Q(x,y)
удовлетворяют условию
 в этом случае общее решение диф-го ур-я
F(x,y)=0
находится по формуле F(x,y)=
в этом случае общее решение диф-го ур-я
F(x,y)=0
находится по формуле F(x,y)= =C.
Интегрирующий множитель: если в ур-е
P(x,y)
и Q(x,y)
не удовлетворяют условию
=C.
Интегрирующий множитель: если в ур-е
P(x,y)
и Q(x,y)
не удовлетворяют условию
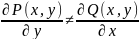 но можно подобрать множитель M(x,y)
такой чтобы прии умножение данное
условие стало выражаться M(P(x,y)dx+
Q(x,y)dy)=dF(x,y).
Тогда общ. решение такого ур-я находится
так же как и в предыдущем случае.
но можно подобрать множитель M(x,y)
такой чтобы прии умножение данное
условие стало выражаться M(P(x,y)dx+
Q(x,y)dy)=dF(x,y).
Тогда общ. решение такого ур-я находится
так же как и в предыдущем случае.
7.ДУ
высших порядков. Общие и частные решения.
Задача Коши. Теорема сущ. един- ственности
решения зада- чи Коши. ДУ
II-го
порядка умеет вид: F(x,y,y’,y’’)=0.
Если оно разрешено относительно
производной приводится к виду
y’’=f(x,y,y’).
Общим решением ДУ II
порядка наз-ся ф-я y=y(x,C1,C2)
которая при подставлении в ур-е при
любых значениях постоянных C1
и C2
превращает его в тождество. Частным
решением ДУ II
порядка наз-ся решение получаемое из
общего при конкретных значениях
постоянных C1
и C2.
График решения ДУ II
порядка наз-ся интегральной кривой
данного ур-я. частное решение ДУ II
порядка нах-ся из общего решения с
помощью начальных условий:
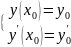 .
Начальные условия позволяют найти
значение постоянных C1
и C2.
Задача отыскания частного решения
наз-ся задачей Коши.
Для ДУ II
порядка задача Коши состоит в том, чтобы
найти интегральную кривую проходящую
через заданную точку M0(x0,y0)
в заданном направлении y0’.
Теорема сущ. и единственности решения.
Если ф-я f(x,y,y’)
ф-я трех независимых перемен- ных
непрерывна в области содержащей точку
M0(x0,y0,y0’)
то ДУ: y’’=f(x,y,y’)
имеет решение y=y(x)
удовлетворяющее условиям y(x0)=y0;
y’(x0)=y0’
кроме того если непрерывны частные
производные
.
Начальные условия позволяют найти
значение постоянных C1
и C2.
Задача отыскания частного решения
наз-ся задачей Коши.
Для ДУ II
порядка задача Коши состоит в том, чтобы
найти интегральную кривую проходящую
через заданную точку M0(x0,y0)
в заданном направлении y0’.
Теорема сущ. и единственности решения.
Если ф-я f(x,y,y’)
ф-я трех независимых перемен- ных
непрерывна в области содержащей точку
M0(x0,y0,y0’)
то ДУ: y’’=f(x,y,y’)
имеет решение y=y(x)
удовлетворяющее условиям y(x0)=y0;
y’(x0)=y0’
кроме того если непрерывны частные
производные
 то решение единственное.
то решение единственное.
8.ДУ
допускающие понижение порядка. 1)
тип ур-ний y’’=f(x)-если
правая часть содержит функцию y
и её производную y’
по определению 2-х производных y’’=(y’)’= ;
;
 ;
;
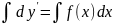 ;
y’=
;
y’= +C1;
y’=
+C1;
y’=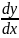 ;
;
 ;
dy=(
;
dy=(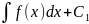 )dx;
)dx;
 ;
y=
;
y= y=
y=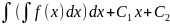 Вычисляя интеграл находим общее решение.
2) тип ур-ний y’’=f(x,y’)
– правая часть ур-ний не содержит явным
образом функцию y.
В этом случае для понижения порядка
делаем подстановку y’=P(x)
где P(x)
неизвестная ф-ия y’’=P’(x).
P’=f(x,p);
P’=
Вычисляя интеграл находим общее решение.
2) тип ур-ний y’’=f(x,y’)
– правая часть ур-ний не содержит явным
образом функцию y.
В этом случае для понижения порядка
делаем подстановку y’=P(x)
где P(x)
неизвестная ф-ия y’’=P’(x).
P’=f(x,p);
P’= ;
;
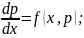 dp=f(x,p)dx.
Интегрируя ур-я находим сначала p
затем делая обратную замену p
на y’
и интегрируя полученное ур-е находим
общее решение. 3) тип ур-ний y’’=f(x,y,y’)
– правая часть не содержит явным образом
аргумент x.
Для понижения порядка делаем замену
y’=P(y);
y’’=P
dp=f(x,p)dx.
Интегрируя ур-я находим сначала p
затем делая обратную замену p
на y’
и интегрируя полученное ур-е находим
общее решение. 3) тип ур-ний y’’=f(x,y,y’)
– правая часть не содержит явным образом
аргумент x.
Для понижения порядка делаем замену
y’=P(y);
y’’=P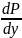 ;
P
=f(y,P)
интегрируя понижаем порядок ур-я и
после обратной замены находим общее
решение.
;
P
=f(y,P)
интегрируя понижаем порядок ур-я и
после обратной замены находим общее
решение.
9. Линейные ДУ (ЛОДУ) 2-го порядка. Свойства решений ЛОДУ 2-го порядка. ДУ 2-го порядка называется линейным, если оно содержит функцию y, её производные y’ и y’’ и не содержит их произведений. Линейное уравнение имеет вид: y’’+p(x)y’+q(x)y=f(x). Если правая часть уравнения = 0, то уравнение называется однородным, а если не равно 0, то неоднородным. ЛОДУ обладает следующими свойством: если y1(x) и y2(x) – два решения этого уравнения, то их линейная комбинация y=C1*y1(x)+C2*y2(x) так же является решением однородного уравнения. 10. Теорема о структуре общего решения ЛОДУ 2-го порядка. Для доказательства необходимо 2-а раза продифференцировать это выражение и подставить y’ и y’’ в левую часть однородного уравнения. В результате должно получиться тождество. 2-а решения ЛОДУ y1(x) и y2(x) называется линейно зависимыми, если их отношение равно постоянному числу. y1(x)/y2(x)=const, если же не равно const, то решение линейно независимо. Сумма 2-х линейно независимых решений ЛОДУ составляет общее решение этого уравнения, таким образом yодн=С1*y1(x)+C2*y2(x).
11. Линейные неоднородные ДУ 2-го порядка. Свойства решений ЛНДУ. Теорема о структуре общего решения ЛНДУ. Для ЛНДУ y’’=p(x)y’+q(x)y=f(x) справедлива следующая теорема: общее решение ЛНДУ равно сумме общих решений соответствующего однородного уравнения и какого-либо частного решения исходного неоднородного уравнения. y’’+p(x)y’+q(x)y=0. Общее решение ЛНДУ: yодн=C1*y1(x)+C2*y2(x)
y=yодн+y*, где y*-частное решение ЛНДУ(структура общего решения ЛНДУ).
12. Метод вариации произвольных постоянных нахождения частного решения ЛНДУ 2-го порядка. Метод неопределённых коэффициентов применим только в тех случаях, когда правая часть ЛНДУ f(x) является либо многочленом, либо показательной функцией, либо тригонометрической функцией (sin и cos). В тех случаях когда правая часть другая применяется метод вариации произвольных постоянных. Пусть дано ЛНДУ y’’+py’+qy=f(x) c постоянными коэффициентами. Запишем соответствующее ЛОДУ: y’’+py’+qy=0 и пусть общее решение ЛОДУ имеет вид yодн=C1*y1(x)+C2*y2(x), где y1(x) и y2(x) – два линейных независимых решения, С1 и С2 – произвольные постоянные. Заменим в общем решении С1 и С2 неизвестными функциями С1(х) и С1(х) и будем искать частное решение исходного ЛНДУ в виде: у*=С1(х)*у1(х)+ С2(х)*у2(х), где у1 и у2 – решения соответсующего ЛОДУ, а С1 и С2 – функции неизвестных. Если у* является решением ЛНДУ, то при подставлении в правую часть ЛНДУ у*, (у*)’, (y*)’’ должно получится тождество. Дифференцируем 2 раз у*. (y*)’=C1’(x)*y1(x)+C1(x)*y1’(x)+C2’(x)*y2(x)+C2(x)*y2’(x)=(C1’(x)*y1(x)+C2’(x)*y2(x))+C1(x)*y1’(x)+C2(x)*y2’(x). Выберем функции C1(x) и С2(Х) таким образом, чтобы сумма, стоящая в скобках была равна 0. С1’(x)*y1(x)+C2’(x)*y2(x)=0. В результате (y*)’=C1(x)*y1’(x)+C2(x)*y2’(x); (y*)’’=C1’(x)*y1’(x)+C1(x)*y1’’(x)+C2’(x)*y2’(x)+C2(x)*y2’’(x). C1’(x)*у1’(x)+С1(х)*y1’’(x)+C2’(x)*y2’(x)+C2(x)*y2’’(x)+p(C1(x)*y1’(x)+C2(x)*y2’(x))+q(C1(x)*y1(x)+C2(x)*y2(x))=f(x)C1(x)*(y1’’(x)+py1’(x)+qy1(x))(скобка равна 0)+С2(х)(у2’’(x)+py2’(x)+ qy2(x))(скобка равна 0)+С1’(x)*y1’(x)+C2’(x)*y2’(x)=f(x). Так как y1(x) и y2(x) являются решениями ЛОДУ, то
С1’(x)*y1(x)+C2’(x)*y2(x)=0
C1’(x)*y1’(x)+C2’(x)*y’(x)=f(x)
y*=C1(x)*y1(x)+C2(x)*y2(x)
Таким образом для того чтобы найти функции С1(х) и С2(х) необходимо решить вышестоящие уравнения. Найти С1’(х) и С2’(x). Затем их проинтегрировать, найти C1(x) и С2(x) и подставить в частное решение y’.
13. ЛОДУ с постоянными коэффициентами. Характеристическое уравнение. Нахождение фундаментальной системы решений.
Пусть необходимо найти общее решение y’’+py’+qy=0, где p и q – const. Общим решением такого ур-ия будет функция y=C1*y1+C2*y2, где у1 и у2 – линейные независимые решения. Для нахождения частных решений y1 и у2 используем следующий метод: предположим, что у=e^kx, где k=const является частным решением ур-ия. Найдём производные у’=k*(e^kx) и y’’=k^2*e^kx и подставим в исходное уравнение. k^2*e^kx+p*k*e^kx+q*e^kx=0; e^kx*(k^2+p*k+q)=0. Подберём условие при котором это равенство выполняется, так как e^kx не равна 0, то k^2+p*k+q=0 – характеристическое уравнение по отношению к однородному уравнению. Получим квадратное уравнение при решении которого возможны следующие случаи: 1)корни уравнения действительные и различные(k1 не равно k2 и принадлежит R(Д больше 0), в этом случае e^k1x и e^k2x линейно независимые. e^k1x/e^k2x=e^(k1-k2)x не равно const, поэтому общее решение однородного уравнения можно записать: y(одн)=C1*e^k1x+C2*e^k2x. 2)k1=k2=k принадлежит R. В этом случае общее решение ЛОДУ записывается в виде y=C1*e^kx+C2*x*e^kx, то есть для второго частного решения добавляется множитель х. Решение линейно независимо. (х*e^kx)/e^kx=0 не равно const. 3)корни характеристического уравнения комплексные(комплексно-сопряжённые). k1=альфа+бета*i и k2=альфа-бета*i. Тогда решение однородного уравнения и имеет вид y=(e^альфа*x)*(C1*cos(бета*х)+C2*sin(бета*x).
14. ЛНДУ с постоянными коэффициентами со специальной правой частью. Метод неопределённых коэффициентов нахождения частного решения ЛНДУ. Пусть необходимо найти общее решение неоднородного уравнения y’’+py’+qy=0. Известно, что общее решение ЛНДУ находится как сумма общего решения соответствующего ЛОДУ и частного решения ЛНДУ. у=у(о)+у*. Рассмотрим способ отыскания у* методом неопределённых коэффициентов. Данный метод позволяет находить частное решение ЛНДУ, если известна структура этого решения, зависящая от структуры правой части ЛНДУ f(x). 1)если правая часть ЛНДУ f(x)=P(x), гду P(x) – многочлен некоторой степени переменной x, то у* необходимо искать в виде: а)у*=Q(x), если число 0 не является корнем характеристического ур-ия; б)у*=xQ(x), если 0 является однократным корнем ур-ия; в)у*=x^2*Q(x), если 0 – двухкратный корень характеристического уравнения; Q(x) – многочлен той же степени, что и P(x), только с неизвестными коффициентами. 2)правая часть ур-ия представляет собой показательную функцию А*(е^альфа*x)=F(x), где A и альфа=const. Тогда у* ищем в виде: а)у*=B*(e^альфа*х), если число альфа не является корнем характеристического уравнения; б)y*=B*x*(e^альфа*х), если альфа – однократный корень характеристического ур-ия; в)у*=В*(х^2)*(е^альфа*х), если альфа – двукратный корень характеристического уравнения. 3)правая часть уравнения имеет вид f(x)=(e^2x)(Acos(бета*х)+Вsin(бета*х)); альфа+-бета*i, тогда у*ищем в виде: а)y*=(e^альфа*x)*(A1cos(бета*х)+В1sin(бета*х)), если альфа+-бета*I не является корнями характеристического ур-ия; б)y*=x*(e^альфа*х)*(A1cos(бета*х)+В1sin(бета*х), если альфа+-бета*i – корни характеристического уравнения. 4)правая часть ур-ия имеет вид: f(x)=(e^альфа*х)*(P(x)cos(бета*х)+Q(x)sin(бета*х)), где P и Q – многочлены, тогда у* в ищем виде: а)у*=(e^альфа*х)*(P1(x)*cos(бета*х)+Q1(x)*sin(бета*х)), если альфа+-бета*i не являются корнями характеристического уравнения; б)у*=х*(е^альфа*х)*(P1(x)*cos(бета*х)+Q1(x)*sin(бета*х), если альфа+-бета*I – корни характеристического ур-ия, где P1(x) и Q1(x) – многочлены той же степени что и степень из многочлена. 5)если правая часть ЛНДУ представляет собой сумму 2-х функций f(x)=f1(x)+f2(x), где f1 и f2 относятся к одному из предыдущих 4 типов, то у* так же ищем в виде суммы 2-х решений у*=у1*+у2*, где у1* - правая часть f1(x), а у2* - левая часть f2(x).
15. ДУ n-го порядка. Решение ЛДУ с постоянными коэффициентами любого порядка производятся аналогично решению ур-ий 2-го порядка. Пусть необходимо найти общее решение ур-ия у(n-го порядка)+p1*y(n-1-го порядка)+…*pn*y=0, где p1 и p2 … pn – постоянные числа. Данное уравнение называется ЛОДУ n-го порядка с постоянными коэффициентами. Для его решения составляется соответсвующее характерестическое уравнение. k^n+p1*k^n+…+pn-1^k+pn=0. Если все корни характеристического уравнения действительные и различные, то есть k1 не равно k2 не равно kn принадлежит R, то общее решение ЛОДУ записывается в виде: у(одн)=С1*(e^k1*x)+C2* (e^k2*x)+…+Cn*(e^kn*x). Если корни повторяются, то к кратным корням будет соответствовать часть решения: у(одн)=С1*(e^k*x)+C2*x*(e^k*x)+C3*x^2*(e^k*x). К каждой паре комплексных корней альфа+-бета*i будет соответсвовать часть решения вида: у(одн)=(e^альфа*х)*(С1*cos(бета*х)+С2*sin(бета*х). Аналогично решается ЛНДУ n-го порядка с постоянными коэфициентами.
16. Системы ДУ уравнений. Рассмотрим систему 2-а линейных ЛДУ 1-го порядка с постоянными кофициентами.
dx/dt=a1*x+b1*y+фи1(t)
dy/dt=a2*x+b2*y+фи2(t), где t – аргумент, фи1(t) и фи2(t) – заданные функции, a1, b1, a2, b2 – const, x(t) и y(t) – искомые функции. Данная система может быть приведена к одному ЛДУ 2-го порядка с постоянными коэффициентами. Продефференцируем обе части первого ур-ия системы по аргументу t: (d^2)x/dt^2=a1*(dx/dt)+b1*(dy/dt)+фи1’(t). Подставим dy/dt из второго ур-ия системы: (d^2)x/dt^2=a1*(dx/dt)+b1*(a2*x+b2*y+фи2(t))+фи1’(t)=a1*dx/dt+b1*a2*x+b1*b2*y+b1*фи2(t)+фи1’(t). Из первого ур-ия системы выразим у: у=(1/b)*((dx/dt)-a1*x-фи1(t)). Подставляем вместо у: (d^2)x/dt^2=a1*(dx/dt)+b1*a2*x+b1*b2*(1/b1)*((dx/dt)-a1*x-фи1(t))+b1*фи1’(t)=a1*(dx/dt)+b1*a2*x+b2*(dx/dt)-a1*b2*x-фи1(t)*b2+b2*фи2(t)+фи1’(t);
((d^2)x/dt^2)-(a1+b2)*(dx/dt)+(b2*a1-b1*a2)*x=b1*фи2(t)-b2*фи1(t)+фи1’(t) больше f(t);
((d^2)x/dt^2)+p*(dx/dt)+q*x=f(t);
xt’’=p*xt’+q*x=f(t). Решая полученное уравнение 2-го порядка находим общее решение х=х(t,C1,C2), затем подставляя в у находим у=у(t,C1,C2).
17.Числовой
ряд. Если
числа а1,а2…аn
образуют
бесконечную числовую последовательность,
то выражение вида а1+а2+…+аn=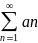 называют числовым
рядом.
называют числовым
рядом.
Числа а1,а2…аn называют членами ряда аn-общий член ряда, является функцией от n.
Если известно аналитическое выражение этой функции, то задавая n последовательно значение 1,2,3 и т.д. можно найти сколько угодно членов ряда, сумма n –первых членов ряда называется n-ой частичной суммой ряда Sn=а1+а2+…+аn. Частная сумма Sn является переменной величиной, т.е. функцией натурального числа n.
S1=a1
S2=a1+a2
Sn=a1+a2+…+an
Если
бесконечная послед-ть частичных сумм
S1,S2,Sn
имеет конечный придел S
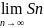 =S,
то в этом случае ряд сходится, число S
называется суммой
сходящегося ряда.
Если частичная сумма Sn
не имеет конечного предела при
=S,
то в этом случае ряд сходится, число S
называется суммой
сходящегося ряда.
Если частичная сумма Sn
не имеет конечного предела при
 ,
то ряд называется расходящимся.
Если ряд сходится и его сумма равна S,
то разность S-Sn
называется n-ым
остатком ряда,
обозначается Rn=an+1+an+2+…
,
то ряд называется расходящимся.
Если ряд сходится и его сумма равна S,
то разность S-Sn
называется n-ым
остатком ряда,
обозначается Rn=an+1+an+2+…
Геометрический
ряд Sn=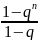 ,
|q|<1
сходится, |q|>=1
расходится.
,
|q|<1
сходится, |q|>=1
расходится.
Гармонический
ряд расходится
 .
.
Необходимый признак сходимости ряда.
Если
ряд сходится, то общий член ряда an
стремится к нулю, ряд
сходится
 ,
если необходимый признак не выполняется,
то ряд
расходится.
,
если необходимый признак не выполняется,
то ряд
расходится.
Основные св-ва сходящихся рядов.
Если ряд а1+а2+…+аn сходится и имеет сумму S, то его можно почленно умножить на одно и тоже число С-const, при этом получится ряд: Ca1+Ca2+…+Can=CS.
Сходящиеся
ряды можно почленно складывать и
вычитать а1+а2+…+аn А,
b1+b2+…+bn
B;
(а1+b1)+(а2+b2)…
А,
b1+b2+…+bn
B;
(а1+b1)+(а2+b2)…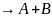 ,
(а1-b1)+(а2-b2)…
,
(а1-b1)+(а2-b2)…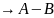 .
.
Если рад сходится, то сходится и ряд полученный из данного путем приписывания или отбрасывания любого конечного числа его членов.
Достаточные признаки сходимости.
Признак сравнения. Пусть даны 2 ряда с положительными членами а1+а2+…+аn(1), b1+b2+…+bn(2). И выполняется условие: члены первого ряда не превосходят соответствующих членов следующего ряда ai<bi, тогда справедливы следующие утверждения, если больший ряд сходится, то и меньший ряд сходится 2(сх) 1(сх), если меньший ряд расх., то и больший ряд расх. (1)расх (2)расх.
Признак
сравнения.
Если при
существует конечный отличный от нуля
предел отношения общих членов первого
и второго ряда
 ,
то эти ряды одновременно сх-ся и расх.
,
то эти ряды одновременно сх-ся и расх.
18. Интегральный признак сходимости знакоположительных рядов (Признак сходимости Каши).
Пусть
дан ряд с положительными членами где
ai>=0
если ф-я f(x)(1;+ )
явл. непрерывной, положительной и
монотонно убывающей, то числовой ряд
где an=f(n)
сходится, если сходится несобственный
интеграл
)
явл. непрерывной, положительной и
монотонно убывающей, то числовой ряд
где an=f(n)
сходится, если сходится несобственный
интеграл
 и ряд расходится если соответствующий
несобственный интеграл расходится.
и ряд расходится если соответствующий
несобственный интеграл расходится.
19.
Признак сходимости Даламбера. Пусть
дан ряд с положительными членами
а1+а2+…+аn,
если существует
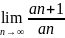 =L,
то возможны следующие случаи: а) при
L<1
сх., б) при L>1
расх. В) при L=1
о сходимости ряда ничего сказать нельзя,
требуется исследование с помощью других
признаков (например сравнения).
=L,
то возможны следующие случаи: а) при
L<1
сх., б) при L>1
расх. В) при L=1
о сходимости ряда ничего сказать нельзя,
требуется исследование с помощью других
признаков (например сравнения).
20.
Знакочередующиеся ряды. Признак
Лейбница. Если
любые два рядом стоящих члена ряда
имеют противоположные знаки, то такой
ряд называется знакочередующимся.
Признак Лейбница. Если члены знакочеред-ся
ряда монотонно убывают по абсолютной
величине и общий член ряда стремится
к нулю при
,
то ряд сходится и его сумма по абсолютной
величине не превосходит абсолютной
величины первого члена ряда: 1)
|а1|>|а2|>…>|аn|,
2) =0.
=0.
21.Знакопеременные ряды. Признак абсолютной сходимости. Понятие условной сходимости. Если среди членов данного ряда есть положительные так и отрицательные (причем тех и других неограниченное кол-во), то такой ряд называется знакопеременным.
Признак абсолютной сходимости. Пусть дан ряд с членами произвольных знаков (1) а1+а2+…+аn и составим ряд из абс-х величин членов исходного ряда (2) |а1|+|а2|+…+|аn|. Исходный ряд (1) называется абс-о сходящимся если сходится как сам ряд так и ряд из абсолютных величин (2).
(1)Абс.
Сходится (2) сходится
(2) сходится
(1)Усл. Сх-ся если сам ряд сходится а ряд из абсолютных величин расходится
(1)Усл. Сх-ся (2)расх
22.Функциональные ряды. Основные понятия. Область сходимости. Сумма функционального ряда. Функциональным рядом называется выражение состоящее из этих функций
U1(X)+ U2(X) +… Un(X)…. Σ Un(X). Функциональный ряд при одних значениях параметра x может оказаться сходящимся а при других расходящимся числовым рядом.Если ф-ый ряд сх-ся при X=X0 ,то ряд сх-ся в точке X0 . Область сходимости-совокупность всех значений переменной X при которых этот ряд сх-ся.
23 Степенной ряд.Интервал и радиус сходимости. Если члены фун-го ряда явл-ся степенными функциями аргумента X , то ряд называется –СТЕПЕННЫМ
A0 + A1X+ A2X2…+ AnXn…= Σ AnXn - основной степенной ряд (сходится при x=0) Интервал сходимости - интервал от –R до R он симметричен относительно нулевой точки.Что бы найти область сходимости сначала нужно найти интервал сходимости от –R до R затем выяснить вопрос о сх-ти ряда на концах интервала. Радиус сходимости – R. Способ нахождения R=Lim [ An / An+1]
24 Теорема о почленном интегрировании и диффиренцировании ряда (теорема Абеля). Если степенной ряд сх-ся при X=X0 то он сх-ся абсолютно при любом значении переменных X удовлетворяющий неравенству [X]< [X0].Если же степенной ряд расх-ся при X=X0 , то он расходится при любом значении X удовлетворяющем неравенству [X]> [X0]
25. Разложение функций в степенные ряды. Ряды Тейлора и Макларена. Известно, что сумма степенного ряда в интервале сходимости этого ряда является непрерывной и бесконечное число раз дифференцируемой функцией. Возникает обратный вопрос: когда можно представить заданную функцию f (x) в виде суммы некоторого степенного ряда?
Всякая
функция бесконечное число раз
дифференцируемая в интервале![]() , т.е.
, т.е.
![]() , может быть разложена в этом интервале
в сходящийся к ней бесконечный степенной
ряд – ряд Тейлора
, может быть разложена в этом интервале
в сходящийся к ней бесконечный степенной
ряд – ряд Тейлора
![]()
если в этом интервале выполняется условие
![]()
Здесь
Rn(x) – остаточный член формулы Тейлора,
![]()
При x0 = 0 из (42) получаем так называемый ряд Маклорена:
![]()
