Единицы измерения

В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1В = 1 Дж/Кл (L²MT⁻³I⁻¹). В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг. Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ

Напряжённость электрического поля

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

.

Также иногда называется силовой характеристикой электрического поля.

Математически зависимость вектора от координат пространства сама задаёт векторное поле.

Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр).

Напряжённость электрического поля точечного заряда Для системы си

Используя потенциалы

К примеру, для точечного заряда, исходя из закона Кулона Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю:

.

В силу центральной симметрии поля точечного заряда:

.

Как и следовало ожидать, результаты полностью совпали.

2) Теорема Гаусса для электрического поля

Теорема Гаусса

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.

Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Следствия из теоремы Гаусса

• Следствием теоремы Гаусса является теорема Ирншоу.

• Электростатическое поле, создаваемое внешними зарядами внутри эквипотенциальной поверхности (например, внутри хорошо проводящей поверхности) равно нулю. Это свойство служит обоснованием экранирования высокочувствительных приборов от электрических помех заключением их в замкнутую проводящую оболочку. Хотя для доказательства аналогичного утверждения в общем случае переменных полей теоремы Гаусса недостаточно (?).

Формулировка теорему Ирншоу

Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.

• Подразумевается, что точечные заряды «непроницаемы», то есть не могут занимать одно и то же положение в пространстве (то есть, подразумевается, что в этом случае прежде, чем точечные заряды займут такое положение, между ними начнут действовать не-кулоновские силы, например, силы упругости поверхностей — если рассматривать точечный заряд как предельный случай маленького тела конечных размеров^[1]); иными словами, очевидные случаи равновесия с совпадающими по пространственному положению положительным и отрицательным зарядами по условию теоремы исключаются из рассмотрения. Это можно мотивировать альтернативным «непроницаемости» способом тем, что такие случаи тривиальны и поэтому не интересны, а также физически сомнительны (подразумевают бесконечную энергию взаимодействия зарядов при таком положении).

• В формулировке теоремы могут быть добавлены «внешние» электростатические поля (создаваемые закрепленными источниками).

• Теорема сама по себе ничего не утверждает о том, что равновесие вообще возможно. Однако нетрудно найти примеры, показывающие, что равновесные конфигурации точечных зарядов (неустойчивые) могут существовать.

3)

Расчет напряженности поля сферически симметричного распределения заряда

Способ расчета с помощью теоремы Гаусса для любого сферически симметричного распределения заряда в целом сводится к тому, что описано выше для случая точечного заряда (см. параграф о законе Кулона).

Отметим тут только в отношении неточечных источников обладающих сферической симметрией вот что (всё это является очевидными следствиями применения описанного там метода):

1. Сферически симметричный заряд с концентрической сферической пустотой (или незаряженной областью) в середине, не создает внутри этой пустоты поля (напряженность поля там равна нулю).

2. Вообще поле на расстоянии r от центра создается только теми зарядами, которые находятся глубже к центру. Это поле можно рассчитать по закону Кулона: E = KQ / r², только под Q здесь следует понимать суммарный заряд шаровой области радиусом r (а это означает, что зависимость от r в итоге отличается от кулоновской, поскольку с ростом r растет Q, по карйней мере пока r не больше радиуса всей заряженной области — если только она в свою очередь конечна).

3. При r, больших радиуса заряженной области (если он конечен), выполняется самый обычный закон Кулона (как для точечного заряда). Это объясняет, например, почему обычный закон Кулона работает для равномерно заряженных шаров, сфер, планет со структурой близкой к сферически симметричной даже вблизи их поверхности (например, почему вблизи поверхности Земли гравитационное поле достаточно близко к полю точечной массы, сосредоточенной в центре Земли).

4. В интересном частном случае равномерно заряженного шара, его электрическое (или гравитационное) поле оказывается внутри шара пропорциональным расстоянию до центра.^[21]

Расчёт напряжённости поля бесконечной плоскости

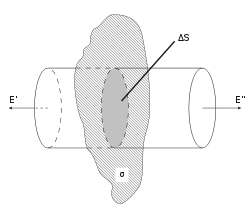
Рассмотрим поле, создаваемое бесконечной однородно заряженной плоскостью с везде одинаковой поверхностной плотностью заряда σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью ΔS каждое), расположенными относительно плоскости симметрично (см. рисунок).

В силу симметрии:

1. Все векторы напряжённости поля (в том числе E' и E'') — перпендикулярны заряженной плоскости: действительно, в силу вращательной симметрии задачи, вектор напряжённости при любом повороте относительно оси, перпендикулярной плоскости, должен переходить в себя, а это возможно для ненулевого вектора только если он перпендикулярен плоскости. Из этого следует (кроме прочего), что поток напряжённости поля через боковую поверхность цилиндра равен нулю (так как поле направлено везде по касательной к этой поверхности).

2. E' = E'' = E.

Поток вектора напряжённости равен (в силу (1)) потоку только через основания цилиндра, а он, в силу того, что E' и E'' перпендикулярны этим основаниям и в силу (2), равен просто 2EΔS.

Применив теорему Гаусса, и учитывая Q = σΔS, получим (в системе СИ):

из чего

4) Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

(13.18)

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

Из выше сказанного следует, что электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал , на близко расположенную эквипотенциальную поверхность, имеющую потенциал (рис. 13.16).

Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения С другой стороны . Из этих уравнений получаем

(13.22)

Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

5)