32. Коєфіцієн кореляції та його властивості
Тісноту кореляційного зв’язку показує коеф. Кореляції.
, де - коваріація , та - середньоквадратичне відхилення по х та у.
Властивості
При =0, лінійно кореляційного зв’язку між х та у не існує, але нелінійний може існувати
завжди належить проміжку [-1;1]( -1 1)
При =1 існує лінійна пряма функціональна залежність між Х таУ, а якщо =-1, то обернена пряма функціональна залежність
При зростанні [0;1] лінійна кореляційна залежність між та Х та У наближене до лінійної функцірнальної залежності, тобто зростає.
33.Функція розподілу ймовірностей та щільність ймовірностей системи
34.Двовимірний нормальний закон розподілу.
Законом
розподілу двовимірної ВВ наз. Передік
можливих значень цієї величини (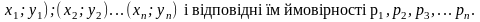
Закони багатовимірної ВВ задаються:таблично і графічно.
35. Біноміальний закон розподілу двв, числові характеристики
ДВВ Х має біноміальний закон розподілу, якщо вона приймає значення 0,1,…n, з ймовірностями які обчислюються за формулою.
,
де q=1-p
Цей закон використовуэться в схемы Бернуллі, тобто у випадку незалежності випробувань в кожному з яких деяка подія зявляється з однаковою ймовірністю р.
Числові характеристики біноміального закону розподілу:
1.М(Х)=n*p
2.Д(Х)=n*p*q
3.
Біноміальний закон розподілу використовується в теорії й практиці статистичного контролю якості продукції, при описуванні фін системи масового обслуговування населення, в теорії стрільби.
36.Пуасонівський закон розподілу двв, числові характеристики.
Закон розподілу Пуассона – це якщо ДВВ Х приймає значення 0,1,2,…n(нескінченна кількість значень) і ймовірність обчислюється за формулою:
Цей
розподіл використовується в схемі
Бернуллі якщо n
а р(q)
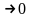і являється граничним випадком
Біноміального закону розподілу.
Закон Пуассона наз. Законом малоймовірних явищ.По закону Пуассона розподілені кількість збоїв на автоматній лінії, кількість забоїв складної системи в нормальному режимі використання.
37.Геометричний закон розподілу Двв, числові характерист.
Геометричний
закон росподілу стосується використов
при з’якуванні ймовірн першого настання
події. Число проведених спроб має
геометричн закон розподілу, якщо ймовірн
його можливих значень рівна: Рк=р*qk-1.
Числові характерис: Математ сподів
(середнє значення сукупності чисел )
M(x)=1/p; дисперсія( міра відхилення значень
ВВ від центру розподілу) D(x)=q*p2;
середнє квадратич відхилен (розсіювання
значень ВВ відносно її математ
сподів) σ=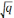
/p.
38.Гіпергеометричн закон розподілу Двв, числові характер.
Гіпергеом
закон розподілу цілочислова величина,
якщо ймовірність можливих значень
обчисл за формулою Рк= Сkn1* Сm-kn-n1 / Сmn.
Нехай є множина однотипних елементів
з числом n1 ознака А (дефект чи помилка)
n-n1=B-решта. Коли з цієї множини беруть m
елементів то число елементів k з ознаки
А чи B, що трапляється з навмання взятих
буде цілочисловВВ за гіпергеометр
законом розподілу. Числов. характер.
М(х)=Σ k*pk; D(x)= Σ k2*pk- М2(х); σ=
.
3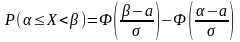
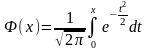9.Рівномірний
закон розподілу Нвв Якщо
відбув попадання ВВ на інтервал пропорційн
до довжини цього інтервалу на осі, то
вона має рівномірн ЗР. Щільність такого
розподілу f(x) = 0 при x≤a; 1/(b-a) при a<x≤b;
0 при x>b. Рівномірн закон розпод легко
моделюв за допомогою функціон перетвор
з величин розподіл рівномірно, можна
отримати величини з довільним ЗР. Числові
х-ки: М(х)=(а+b)/2; D(х)=(b-а)2/12.
4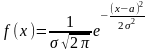
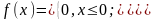0.Нормальний
закон розподілу.
Норм закон розподілу задається щільністю:
f(x). Параметри а і σ, які входять до виразу
щільності розподілу, є відповідно матем
сподіван та середнім квадратич відхил
ВВ. Нормал ЗР широко застосов в матем
статист. Для обчисл ймовірн потрапляння
ВВ, розподіл нормал, на проміжок використ
ф-ція Лапласа
41.Показников закон та його використ в теор надійн та черг. Щільність розподілу ВВ, за показников законом задається формулою: f(x). ВВ з таким законом широко застосов в задачах з теорії надійності та теорії масового обслуговув. Числові характер: M(x)= 1/a; D(x)=1/a2; σ= .
42.Розпод
Стьюдена. Розподіл Фішера
Розпод Стьюдена розподіл ймовірнос, що
виник у задачі оцінки сподів значення
норм розподіл, коли розмір вибірки
малий. Цей розподіл є основою t-тесту
Ст'юдента статист значущості різниці
М(х) двох вибірок, та інтервалу певності
різниці очікуваних значень двох вибірок.
Розподіл Ст'юдента є також частков
випадком узагальн гіперболічног
розподілу. З такими характер: ν >
0 ступені свободи (дійсне); х є (-∞;∞);
Розподіл ймовірн → Ф-ція розпод ймовірн↓
Середнє = 0 для ν>1інакшеØ Медіан 0
Мода=0 Дисперс для ν/(ν-2) при ν>2, інакше
Ø Коефіц асиметрії 0 для ν > 3 Коефіц
асиметрії: 6/(ν-4) при ν>4 Розподіл Фішера
F-розподіл-двопараметр сімейство
абсолютно неперер розподілів. F-розподіл
часто зустріч як розподіл тестової стат
коли нульова гіпотеза вірна, особливо
в тесті відношен правдоподібнос,
найважлив випадок аналіз дисперсії.
Параметри: d1>0 d2>0-ступені свободи;
носій функції xє[0;∞]; розподіл ймовірностей
↓
Ф-ція розпод ймовірн →
Середнє d2/(d2-2), при d2>2
Медіана (d1-2)/ d1 для d1 > 2
Мода d2/(d2+2) Дисперсія
для d2 > 4
