26. Мода, медіана випадкової величини

Мода-значення ВВ, що трапляється найчастіше в сукупності спостережень.

Іншими словами мода є найпоширеніше значення ВВ(ознаки). У дисконтному ряду вона визначається візуально за найбільшою частотою (часткою), а в інтервальному – таким чином визначається модальний інтервал, а конкретне модальне значення розраховується за формулою.

та h – нижня межа та ширина модального інтервалу

- частоти відповідно модального, перед модального та післямодального інтервалів.

Мода неперервного розподілу – це точка максимуму щільності розподілу ймовірностей.

Мода дискретного розподілу-це таке спектральне значення випадкової величини, що наступне та попереднє значення мають менші ймовірності.

Розподіли, що мають дві або більше мод наз. Двомодальними, тримодальними та багтомодальними.

Медіана – характеристика розподілення ВВ. Медіана ділить ряд значень ознаки на дві рівні частини, по обидві частини від неї розміщується однакова кількість од. сукупності.

Медіана позначається або

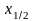
Медіаною функції розподілу F наз. Таке число , що Р(Х< )=P(X> )=0.5

27.Початкові та центральні моменти

Узагальненим числовими характеристиками ВВ є початкові та центральні моменти.

Початковим моментом k-го порядку ВВ Х

Наз. Матем. Сподівання величини

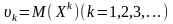
Для ДВВ Х:

Для НВВ Х:

Якщо Х є [a;b] то

Центральним моментом k-го порядку наз. Матем. Сподівання від

Коли k=1,

Коли k=2 ,

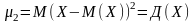
Для ДВВ:

Для НВВ:

Якщо Х є [a;b]

28. Асиметрія, ексцес

Третій центральний момент характеризує асиметрію закону розподілу ВВ.

Якщо , то ВВ Х симетрично розподілена відносно М(Х). Оскільки 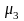має розмірність ВВ в кубі, то вводять безрозмірну величину – коефіцієнт асиметрії.

Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності f(х).Ексцес обчислюється за формулою:

29.Означення багатовимірної випадкової величини

Ми розглядали ВВ Х, які приймали одне можливе числове значення , але є ВВ можливе значення яких визначається 2,3,..n числами. Такі величини наз. Відповідно двовимірні, тривимірні або n-вимірні.

Двовимірні ВВ(Х;У) визн. Двома складовими або компонентами, які утв. Систему двох ВВ.

Якщо складові Х і У дискретні, то двовимірна ВВ наз дискретною а якщо неперервні – неперервними.

30. Означення закону розподілу багатовимірної випадкової ввеличини.

31.Основні числові характеристики для системи двох дискретних випадкових величин.

Під час вивч. Системи двох і більше ВВ доводиться з’ясовувати наявність зв’язку між цими величинами та його характер. З цією метою застосовують кореляційний момент (коваріацію)

Властивості

1)якщо =0, то зв'язок між Х та У, що належить системі (х;у) відсутній.

2)якщо 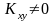, то зв'язок між відп х та у існує.

Тісноту кореляційного зв’язку показує коеф. Кореляції.

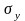, де - коваріація , та - середньоквадратичне відхилення по х та у.

Властивості

При =0, лінійно кореляційного зв’язку між х та у не існує, але нелінійний може існувати

завжди належить проміжку [-1;1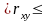]( -1 1)

При =1 існує лінійна пряма функціональна залежність між Х таУ, а якщо =-1, то обернена пряма функціональна залежність

При зростанні 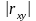[0;1] лінійна кореляційна залежність між та Х та У наближене до лінійної функцірнальної залежності, тобто зростає.