Оценка параметрам закона распределения. Свойства оценок параметрам
Случайное значение искомого параметра, вычисленного на основании данного статистического материала, называют оценкой параметра.
Оценка параметра должна быть состоятельной. Это означает, что при увеличении числа опытов, оценка все более приближается (стремится по вероятности) к точному значению параметра
~ при n .
Оценка параметра должна быть несмещенной, т.е. ее математическое ожидание должно равняться оцениваемому параметру. M[~] = .
Желательно, чтобы оценка параметра была эффективной, т.е. оценка по сравнению с другими должна обладать наименьшей дисперсией.
Сформулированным требованиям обладают следующие точечные оценки основных параметров распределения случайной величины – математического ожидания и дисперсии
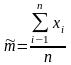
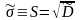
Величина S2 называется исправленной дисперсией, при n > 30 считается, что разница между исправленной и выборочной дисперсией несущественна.
9-10. Задача на доверительный интервал
Вероятность называется доверительной если интересующее нас событие A, происходящее с этой вероятностью, считается практически гарантированным (достоверным). Как правило, близка к единице и выбирается равной 0.9, 0,95, 0,99 или 0,999. Максимальной вероятной погрешностью статистической оценки называется ее максимально возможное отклонение > 0 от оцениваемого параметра, гарантируемое с вероятностью .
оценка мат ожидания , оценка дисперсии
для определения доверительного интервала используют распределение Стьюдента, функция распределения которого S(t,n), в отличии от нормального закона, зависит только от размера выборки n.
Чтобы найти доверительный интервал для оценки математического ожидания по заданной доверительной вероятности, необходимо:
1. Вычислить оценку математического ожидания, вычислить оценку дисперсии S2, а по ней величину S.
2. Для величины по таблиц значений функции распределения Стьюдента определить t;
3. Вычислив , записать доверительный интервал
I = (m~- , m~+ ). (Малая выборка с объемом меньше 30)
Большая выборка, т.е. объем выборки больше 30.
Поскольку m~ есть сумма достаточно большого числа слагаемых, то согласно закону больших чисел она приближенно распределена по нормальному закону.
Функция
Лапласа: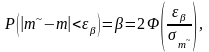 
где среднеквадратическое отклонение
случайной величины m~
можно приближенно положить равным
величине
.
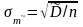Получаем:
Таким образом, чтобы найти доверительный интервал для оценки математического ожидания по заданной доверительной вероятности, необходимо:
1.
Вычислить оценку дисперсии для m~,
а по ней величину
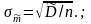
2. Для величины (1+)/2 по таблице приведенной функции распределения Лапласа определить t;
3. Вычислив , записать доверительный интервал I = (m~- , m~+ ).
11. Оценка вероятности по частоте
Пусть в результате опыта фиксируется наступление (или не наступление) события A. После проведения n опытов получена частота наступления этого события р* .
Для достаточно большого числа проведенных опытов можно записать доверительный интервал:
(здесь
использована формула для дисперсии
биномиального закона распределения D
= p(1-p)).
Для малого числа опытов гипотеза о нормальности закона распределения р* неверна и необходимо пользоваться точно известным законом. р* распределена по биномиальному закону (реализуется схема опытов Бернулли). Поскольку биномиальный закон не симметричен, говорят не о доверительном интервале, а о доверительной области. Ее определяют границы /2 и (1 - )/2, где =1 - .
Если в результате n опытов событие A не произошло ни разу, то частота события р* = 0. В этом случае событие A либо невозможно, либо его вероятность весьма мала. Поставим задачу определить доверительные границы для вероятности события A, совместимые с полученными результатами опыта – это событие ни разу не произошло. Не вызывает сомнения, что нижняя граница р1 есть 0. Верхняя же граница р2 может быть оценена на основании следующих соображений. Если в n опытах событие A не произошло ни разу (вероятность (1-р2)n ), то доверительная "совместимость" с этим фактом есть 1-, т.е. (1-р2)n = 1- . Отсюда:
