1. Основные задачи математической статистики

Математическая статистика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.

Задачи математической статистики:

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

1. указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

2. разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:

• оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;

• проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.

Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

 Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.  

2. Первичная обработка данных. Гистограмма

Гистограмма — способ графического представления табличных данных.

Гистограмма в математической статистике - это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.

Построение гистограмм используется для получения эмпирической оценки плотности распределения случайной величины. Для построения гистограммы наблюдаемый диапазон изменения случайной величины разбивается на несколько интервалов и подсчитывается доля от всех измерений, попавшая в каждый из интервалов. Величины каждой доли полагаются значениями, которые принимаются оценкой плотности распределения на соответствующем интервале.

Алгоритм обработки первичных данных: (писал по лекциям, так что неуверен в этом)

1. упорядочить данные

2. разбить на группы/разряды

3. найти частоту. P* (количество чисел в группе делим на общее количество)

4. построение гистограммы

5. нахождение накопленной частоты(сумма частот данного и всех предшествующих интервалов, КУМУЛЯТА)

6. нахождение мат ожидания и дисперсии.

3. Статистическая функция распределения

Функция распределения(в теории вероятностей) — функция, характеризующая распределение случайной величины или случайного вектора. При соблюдении известных условий полностью определяет случайную величину.

Предположим, что изучается некоторая случайная величина  , закон распределения которой в точности неизвестен, и требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величина   подчинена тому или иному закону. С этой целью над случайной величиной   производится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина   принимает определенное значение. Совокупность наблюденных значений величины и представляет собой первичный статистический материал, подлежащий обработке, осмыслению и научному анализу. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом».

Простой статистический ряд представляет собой первичную форму записи статистического материала и может быть обработан различными способами. Одним из способов такой обработки является построение статистической функции распределения случайной величины.

Статистической функцией распределения случайной величины   называется частота события   в данном статистическом материале:

.                                                                  

Для того чтобы найти значение статистической функции распределения при данном  , достаточно подсчитать число опытов, в которых величина   приняла значение, меньшее чем  , и разделить на общее число   произведенных опытов.

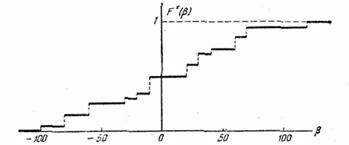(как пример…)

Статистическая функция распределения любой случайной величины - прерывной или непрерывной - представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. Если каждое отдельное значение случайной величины   было наблюдено только один раз, скачок статистической функции распределения в каждом наблюденном значении равен  , где   - число наблюдений.

При увеличении числа опытов  , согласно теореме Бернулли, при любом   частота события   приближается (сходится по вероятности) к вероятности этого события. Следовательно, при увеличении   статистическая  функция распределения   приближается (сходится по вероятности) к подлинной функции распределения   случайной величины  .

Если   - непрерывная случайная величина, то при увеличении числа наблюдений   число скачков функции   увеличивается, самые скачки уменьшаются и график функции   неограниченно приближается к плавной кривой   - функции распределения величины  .