1 Билет (перестановки)
2.1. Перестановки. Инверсия, транспозиция. Четность (нечетность) перестановки.
Возьмем
первые
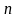натуральных чисел: 1, 2, …,
.
Любой набор
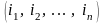этих чисел, расставленных в некотором
порядке, называется перестановкой.
Пример
1. Наборы
,
,
,
,
,
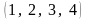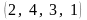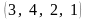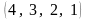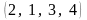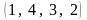представляют собой перестановки первых
четырех натуральных чисел.
Число
различных перестановок из
символов 1, 2, …,
равно
.
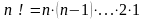Если в некоторой перестановке поменять местами два символа (не обязательно соседние), то получится новая перестановка, Такое преобразование перестановки называется транспозицией.
Пример
2. Перестановка
получается транспозицией чисел 3, 4 из
перестановки
.
Эту транспозицию запишем так:
.
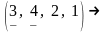В свою очередь, запись
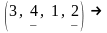
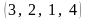означает, что перестановка
получена транспозицией чисел 4, 2 из
перестановки
.
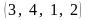В
перестановке
числа
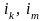составляют инверсию,
если
,
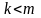но
.
Пример
3. Перестановка
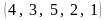содержит 8 инверсий:
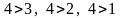- три инверсии;
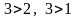- две инверсии;
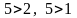- две инверсии;
- одна инверсия. Всего – 8 инверсий.
Перестановка называется четной (нечетной), если она содержит четное (нечетное) число инверсий. Перестановка из примера 3 содержит 8 инверсий, значит она четная.
Любая транспозиция перестановки меняет ее четность.
Пример
4. Рассмотрим
перестановку
,
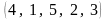полученную транспозицией чисел 3, 1 из
четной перестановки
.
Перестановка
должна быть нечетной. Так оно и есть,
поскольку перестановка
содержит:
- три инверсии и
- две инверсии. Всего – 5 инверсий.
Четность
(нечетность) перестановки
можно также определить по количеству
транспозиций, переводящих эту перестановку
в перестановку
.
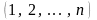Перестановка будет четной (нечетной), если для этого требуется провести четное (нечетное) число транспозиций.
Пример
5. Перестановку
можно перевести в перестановку
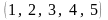с нормальным порядком расположения
чисел следующими тремя транспозициями:
;
;
.
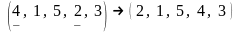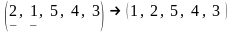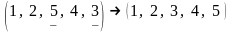Следовательно, перестановка
- нечетная, что согласуется с выводами
примера 4, приведенного выше.
2 Билет (Определитель n-го порядка)
Свойства:
Определитель не изменится, если его строки заменить столбцами, и наоборот.
При перестановке двух параллельных рядов определитель меняет знак.
Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю.
Общий множитель элементов можно вынести за знак определителя.
Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей.
Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение.
Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю.
3 Билет (Определитель с 0 углом)
Определитель треуг. матрицы равен произведению диагональных элементов. Доказать можно разложением по первой строке.