30(41). Разложение логической функции по переменным. Понятие совершенной дизъюнктивной нормальной формы логической функции. Понятие совершенной конъюнктивной нормальной формы логической функции.

Разложение логической функции по переменным

Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма.

Введем обозначение x0=Øx, x1=x. Пусть а - параметр, равный 0 или 1. Тогда xA=1, если x=а, и xA=0, если х¹а.

Теорема. Всякая логическая функция f(x1, . , xn) мо-жет быть представлена в следующем виде:

где n ³ m, а дизъюнкция берется по всем 2m наборам значений переменных х1, ., хm.

Это равенство называется разложением по переменным х1, ., хт. Например, при n=4, m=2 разложение имеет вид:

f(x1, x2, x3, x4)= Øx1 Øx2 f(0, 0, x3, x4) È Øx1 x2 f & (0,1,x3,x4)È x1 Øx2 f(1,0,x3,x4)È x1 x2 f(1,1,x3,x4)

Теорема доказывается подстановкой в обе части равенства произвольного набора всех п переменных.

При m=1 из получаем разложение функции по одной переменной

Ясно, что аналогичное разложение справедливо для любой из п переменных. Другой важный случай — разложение по всем п переменным (т=п). При этом все переменные в правой части (3.4) получают фиксированные значения и функции в конъюнкциях правой части становятся равными 0 или 1, что дает:

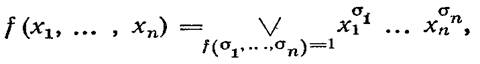
где дизъюнкция берется по всем наборам на которых f=1. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f. СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице f ; каждому единичному набору соответствует конъюнкция всех переменных, в которой Xi взято с отрицанием, если si = 0, и без отрицания, если si = l. Таким образом, существует взаимно однозначное соответствие между таблицей функции f (x1, ., хп) и ее СДНФ, и, следовательно, СДНФ для всякой логической функции единственна (точнее, единственна с точностью до порядка букв и конъюнкций: это означает, что ввиду коммутативности дизъюнкции и конъюнкции формулы, получаемые из предыдущей формулы перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Единственная функция, не имеющая СДНФ – это константа 0.

Формулы, содержащие, кроме переменных (и, разумеется, скобок), только знаки функций дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами (напомним, что знак конъюнкции, как правило, опускается). Предыдущая формула приводит к важной теореме.

Теорема. Всякая логическая функция может быть представлена булевой формулой, то есть как суперпозиция конъюнкции, дизъюнкции и отрицания.

Действительно, для всякой функции, кроме константы 0, таким представлением может служить её СДНФ. Константу 0 можно представить булевой формулой Ø xx.

А почему же формула называется “совершенной”? Совершенной называется потому, что она имеет 4 свойства совершенства.

1. В формуле все конъюнкции разные.

2. В конъюнкции все переменные разные.

3. В одной конъюнкции не встречаются переменные вместе с их отрицанием.

4. В конъюнкции столько переменных, сколько в исходной функции f , то есть n. (Число переменных в функции есть ранг этой функции).

Понятие совершенной дизъюнктивной нормальной формы логической функции

это такая ДНФ, которая удовлетворяет трём условиям: = в ней нет одинаковых элементарных конъюнкций; =в каждой конъюнкции нет одинаковых пропозициональных букв; =каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке. Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. В ячейках строки́   отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии. Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 

Пример

x1 x2 x3 φ( x1, x2, x3) 0  0  0  0  1  1  1  1 0  0  1  1  0  0  1  1 0  1  0  1  0  1  0  1 1  0  1  0  0  1  1  0

Для построения СДНФ выпишем все наборы, на которых функция равна 1: 000, 010, 101, 110. Для каждого набора построим элементарную конъюнкцию, равную единице на этом наборе:  Соединяя эти конъюнкции знаками дизъюнкции, получаем СДНФ заданной функции:  Для построения СКНФ выписываем все наборы, на которых функция равна нулю: 001, 011, 100, 111. Для каждого набора построим элементарную дизъюнкцию, равную нулю на этом наборе: 

Понятие совершенной конъюнктивной нормальной формы логической функции

Конъюнктивной совершенной нормальной формой (КСНФ) называется КНФ содержащая в каждой из перемножаемых сумм все без исключения аргументы.

Пример КСНФ:

Каждая логическая функция может быть записана единственным образом как в виде ДСНФ, так и в виде КСНФ.

ДСНФ тесно связанна с представлением любого комбинационного устройства в виде ряда дешифраторов и элементов ИЛИ. Пусть, например, нужно устройство, которое выдавало бы логическую единицу при подаче на его входы трехразрядных двоичных кодов чисел 3₁₀ и 6₁₀, и логический нуль при любых других трехразрядных кодах. Такое устройство может быть выполнено с помощью двух дешифраторов с ключевыми словами 011 и 110 и элемента ИЛИ.