20) Основные задачи динамики

Первая основная задача динамики

    В основе классической динамики лежат законы, впервые сформулированные и систематически изложенные И.Ньютоном в его «Математических началах натуральной философии».

    В зависимости от того, что нам известно и что необходимо найти, в динамике рассматривают две основные задачи.

    Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.

    При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

где  m  – масса точки;

        a   – ускорение точки;

        F_i  – силы, действующие на точку.

    В зависимости от способа задания движения точки, это уравнение можно записать по-разному.

    Для векторного способа задания движения

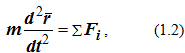
где   r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.

    Для координатного способа задания движения точки

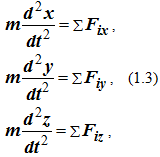
где x = x (t), y = y (t), z = z (t)  – координаты точки, заданные как функции времени.

    Для естественного способа задания движения точки

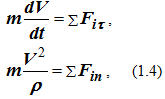
                                               0 = Σ F_ib ,

где  dV/ dt  – проекция ускорения точки на касательную в данной точке (касательное ускорение),  V²/ ρ  – проекция ускорения на нормаль (нормальное ускорение),  

ρ – радиус кривизны траектории. 

    В правой части уравнений – проекции сил на касательную ΣF_iτ , 

нормаль ΣF_in и  бинормаль ΣF_ib .

    По заданному закону движения точки определяются правые части этих уравнений, и далее может быть определена результирующая сила   

– при  координатном способе задания движения:  

– при естественном способе или одна из составляющих сил:

    Направление силы определяется с помощью направляющих косинусов:

cos (α) = R_x / R ,  cos (β) = R _y / R  , cos (γ) = R _z / R   (1.5)

где α , β , γ – углы между направлением силы и осями x , y , z соответственно.

Аналогично определяются углы, которые составляют силы с естественными осями координат.

Вторая основная задача динамики

    Вторая, основная задача динамики точки заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.

    Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

    Уравнение второго основного закона динамики для материальной точки массой m запишется в виде

где a – ускорение точки;

     F_i – силы, действующие на точку, включая реакции связей. 

    Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений 

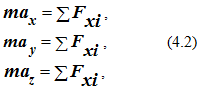
где  a_x , a_y, a_z – проекции ускорения точки на декартовы оси координат;

 F_x, F_y, F_z – проекция i -й силы на соответствующую ось.

    Учитывая, что

получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки или второго порядка относительно координат точки.

    Спроектировав уравнение (4.1) на естественные оси координат, получим следующую систему уравнений: 

                                   

ma_τ = ΣF_τi ,

ma_n = ΣF_ni,

0 = ΣF_bi .

    Учитывая, что

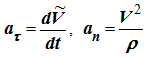
где V – алгебраическое значение скорости, получим

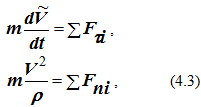                                            0 = ΣF_bi .

    В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых, или в естественных координатах.

    Каждое дифференциальное уравнение дает целый класс решений, отличающихся друг от друга на некоторую постоянную величину. Чтобы получить решение конкретной задачи, должны быть заданы так называемые начальные условия, которые позволяют определить постоянные интегрирования.

Третья или смешанная задача динамики: могут быть неизвестны ни закон движения, ни силы. Нужно определить и то, и другое. К этому классу задач относятся задачи о несвободном движении точки и управляемом движении.

Универсальный метод решения этой задачи – метод множителей Лагранжа . Иногда помогает и выбор удобной системы координат.

22)Система материальных точек. Внутренние и внешние силы.

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом -  , а внутренние -  .

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Внутренние силы обладают следующими свойствами:

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами   и  , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

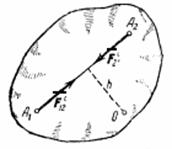
Рис.31

 

2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.18 видно, что  . Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет:

 или  .

Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело.