10) Ускорение Кориолиса

Поворотное ускорение, или ускорение Кориолиса, возникает только при наличии вращения подвижных осей и характеризует быстроту изменения относительной скорости в переносном движении и быстроту изменения переносной скорости в от­носительном движении и состоит из двух равных поворотных компонент

. (61)

Определим, при каких условиях ускорение Кориолиса обращается в ноль. Это имеет место при :

Возникает вопрос о том, как можно подсчитать его алгебраическую величину, компоненты и определить направление:

1. алгебраическая величина

;

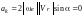2. компоненты в декартовых координатах

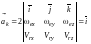
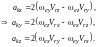(62)

К омпоненты ускорения Кориолиса можно определить и по правилу циклической перестановки для компонент векторного произведения: для нахождения какой-либо компоненты векторного произведения берем компоненту первого со­мно­жителя с индексом, следующим за индексом искомой компоненты, а компоненту второго сомножителя – с ин­дексом, следующим за индексом первого сомно­жи­теля, минус все наоборот.

Направление ускорения Кориолиса легко определить:

а) по правилу правого винта в пространственном случае (рис. 42);

б) правилу Жуковского в плоском случае (рис. 43).Error: Reference source not found

Рис. 42 Рис. 43

11) Вращательное движение твердого тела

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

 φ=φ(t) – уравнение вращательного движения твердого тела.

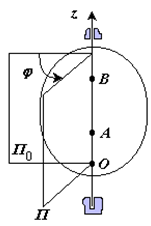
Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту.  За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин).  Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

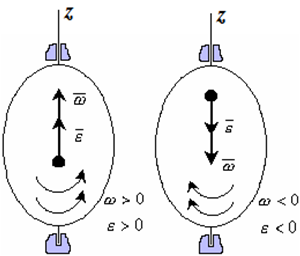
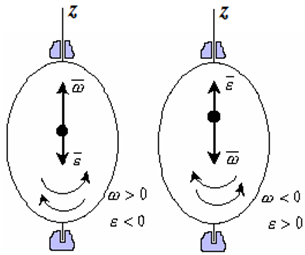
Рис. 1.4

Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону.  Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.

При ε <0 и ω <0 – тело вращается ускоренно  в отрицательную сторону.  Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .

Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.

Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторыω и ε направлены в противоположные стороны.

Если угловая скорость  ω=const, то вращательное движение называется равномерным. Уравнениеравномерного вращения

φ=φ₀+ωt

Если угловое ускорение ε=const, то вращательное движение называется равнопеременным. 

Уравнение равнопеременного вращения

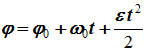
и уравнение, выражающее угловую скорость в любой момент времени

 ω=ω₀+εt

представляют совокупность основных формул вращательного равнопеременного движения тела.