20. Идентификация модели. Необходимое и достаточное условие

Идентификация-установление соответствия между приведённой и структурной формой модели.

Классы структурных моделей:

1.идентифицируемая.Все структурные коэффициенты однозначно определяются через приведённые коэффициенты;

2.сверхидентифицируемая.Стректурные коэффициенты,выражаемые через приведённые коэффициенты, имеют 2 и более числовых значений.

3.неидентиф – струк коэф-ты невоз-но найт по привед коэф-там

Установление неидентифицируемости модели: модель идентиф тольк тогда когда идентиф каждое ее ур-е

Необходимое условие: n=p+1

Уравнение модели идентифицируемо,если количество эндогенных переменных x(ni) этого уравнения на единицу больше количества (pi) предопределённых переменных системы,не входящих в данное уравнение.если n<p+1то ур-е сверхиден, если n>p+1 то ур-е неидентиф

Достаточное условие идентиф-ти модели: Δ≠0, rankA=n-1

Если определитель (Δ) матрицы коэффициентов (А) при переменных системы,не входящих в данное уравнение,не равен нулю и количество эндогенных переменных системы без единицы равно рангу этой матрицы,то уравнение модели идентифицируемо.

Косвенный МНК В настоящее время классическими для решения систем одновременных уравнений является косвенный МНК и двухшаговый МНК. Косвенный МНК основан на получении оценок параметров структурной формы модели по оценкам параметров приведённой формы.Оценки являются состоятельными и несмещёнными в силу применения к каждому уравнению приведённой формы МНК. Алгоритм косвенного МНК:

1)структурная форма модели преобразуется в приведённую форму;

2)с помощью МНК оцениваются параметры приведённой формы;

3)приведённая форма преобразуется в структурную.

Область применения косвенного МНК ограничивается идентифицируемыми системами одновременных уравнений.

Пример: оценить параметры модели идентифицируемой стрн-ной модели на основе условных исходных данных.

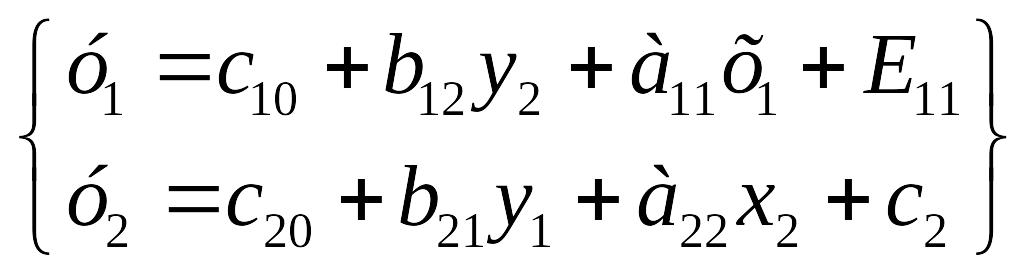n=2, p=1, n=p+1: 2=1+1-

Ур-ния переменные ^{необходимое условие выполнено}

у₁ у₂ х₁ х₂ detA

(1) -1 0 rank A=1

(2) -1 0 1=2-1

^{достаточное условие выполнено}

21 Задачи и этапы эмм

Эк-мат модель исследуемого эк объекта-ео мат описание.Эк-мат модел-ние-исслед-ние эк объектов посредством их мат моделей.

Задачи ЭММ

1)анализ эконом-х объектов и процессов

2)эконимич-ое прогнозиров-ие развития эконом-х процессов

3) выработка управленческих решений на всех уровнях хоз-ой иерархии

Этапы ЭММ

1)анализ законов, описыв-их связи основных объектов(переменных) модели

2 ) теорет-ое исслед-ие построенной мат.модели – реш-ие прямой задачи и, как следствие, исследов-ие св-в эндогенных переменных и их сопоставление с реальными наблюдениями изучаемых явлений.

3)проверка адекват-ти модели, т.е. выяснение того, согласуется ли гипотетич-ая(построенная) мат.модель с моделируемым экон-им процессом.

4)последующий анализ с уточнением мат.модели с учетом накопл-х данных об изучаемом экон-ом процессе.

Математические модели

• Аналитические

• Численные

• Матричные

• Сетевые

• Алгоритмические

ЭМ моделирование-описание знаковыми математическими средствами СЭС.

Основные типы ЭМ моделей:

• По целевому назначению

-теоретика аналитические

-прикладные

• Модели разнообразных математических зависимостей

• По степени включения объекта в моделирование

-микроэконом.

-макроэконом.

• По цели создания и применения

-оптимизационные-балансовые-трендовые-равновесные